题目内容
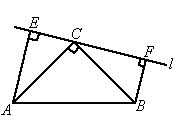
如图所示，已知等腰直角三角形ABC的底边为AB，直线l过直角顶点C，过点A，点B分别作l的垂线AE，BF，E，F两点为垂足．当直线l不与底边AB相交时，
求证：EF=AE＋BF．
答案：略
解析：
解析：
|
证明：∵直线 l过点C，∠ACB=90°，∴∠ACE＋∠BCF=90°， 又∠AEC=90°，∠ACE＋∠CAE=90°， ∴∠CAE=∠BCF， 又∵∠AEC=∠CFB=90°，AC=CB， ∴△ACE≌△CBF， ∴CE=BF，AE=CF， ∴EF=AE＋BF． |
练习册系列答案
智趣暑假温故知新系列答案
英语小英雄天天默写系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
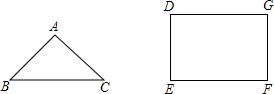
如图所示，已知等腰三角形ABC，AB边的垂直平分线交AC于点D，交AB于E，AB=AC=8，BC=6，求△BDC的周长．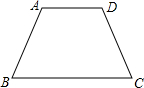
如图所示，已知等腰梯形ABCD中，AD∥BC，下底BC与上底AD的差恰好等于腰长AB，则∠BAD=（ ）