题目内容
已知圆O的直径AB=2cm,过A点的两弦AC=
cm,AD=
cm,则∠CAD所夹圆内部分的面积是______cm2.
| 2 |
| 3 |
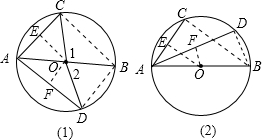
(1)如图(1),连接BC、BD、OC、OD,
∵AB是⊙O的直径,∴∠ACB=∠ADB=90°,
∵OC=OA=
AB=
×2=1,AC=
cm,
∴12+12=(
)2,即OA2+OC2=(AC)2,
∴△AOC是等腰直角三角形,∴S△AOC=
×1×1=
;
∴∠BOC=90°,S扇形BOC=
=
;
在△AOD中,过O作OF⊥AD于F,
∵OA=OD=1,∴AF=DF=
AD=
×
=
.
OF=
=
=
,
∴S△AOD=
×AD×OF=
×
×
=
.
在Rt△AOD中,BD=
=
=1,
∴△BOD是等边三角形,∠BOD=60°,
∴S扇形BOD=
=
.
∴∠CAD所夹圆内部分的面积=S△AOC+S扇形BOC+S△AOD+S△AOD=
+
+
+
=
+
(m2).
(2)同(1),
∠CAD所夹圆内部分的面积=S△AOC+S扇形BOC-S△AOD-S△AOD=
+
-
-
=
+
(m2).
∵AB是⊙O的直径,∴∠ACB=∠ADB=90°,
∵OC=OA=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
∴12+12=(
| 2 |
∴△AOC是等腰直角三角形,∴S△AOC=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠BOC=90°,S扇形BOC=
| 90°π×12 |
| 360° |
| π |
| 4 |
在△AOD中,过O作OF⊥AD于F,
∵OA=OD=1,∴AF=DF=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| ||
| 2 |
OF=
| OA2-AF2 |
12-(
|
| 1 |
| 2 |
∴S△AOD=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| ||
| 4 |
在Rt△AOD中,BD=
| AB2-AD2 |
22-
|
∴△BOD是等边三角形,∠BOD=60°,
∴S扇形BOD=
| 60π×12 |
| 360 |
| π |
| 6 |
∴∠CAD所夹圆内部分的面积=S△AOC+S扇形BOC+S△AOD+S△AOD=
| 1 |
| 2 |
| π |
| 4 |
| ||
| 4 |
| π |
| 6 |
2+
| ||
| 4 |
| 5π |
| 12 |
(2)同(1),
∠CAD所夹圆内部分的面积=S△AOC+S扇形BOC-S△AOD-S△AOD=
| 1 |
| 2 |
| π |
| 4 |
| ||
| 4 |
| π |
| 6 |
2-
| ||
| 4 |
| π |
| 12 |


练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目


 ,
,


