��Ŀ����
����Ŀ���Ķ�������ϣ�
С����������һ�����⣺
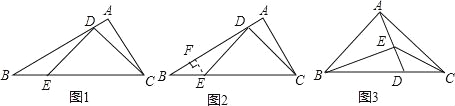
��ͼ1����ABC�У���A=90�㣬��B=30�㣬��D��E�ֱ���AB��BC�ϣ�����CDE=90�㣮��BE=2ADʱ��ͼ1���Ƿ������CD��ȵ��߶Σ������ڣ����ҳ�������֤�����������ڣ�˵�����ɣ�
С��ͨ��̽�����֣�����E��AB�Ĵ���EF������ΪF���ܵõ�һ��ȫ�������Σ���ͼ2�����Ӷ���������⣮
��ش�
��1��С�����ֵ���CD��ȵ��߶��� ��
��2��֤��С�����ֵĽ��ۣ�
�ο�С��˼������ķ����������������⣺
��3����ͼ3����ABC�У�AB=AC����BAC=90�㣬��D��BC�ϣ�BD=2DC����E��AD�ϣ�����BEC=135�㣬��![]() ��ֵ��
��ֵ��
���𰸡���1��DE��2��֤����������3��![]()
��������
�����������1��ֱ��д���𰸣�
��2�����жϳ���ADC=ADC=��FEDFED�����жϳ�FE=AD�������жϳ���FEDFED�ա�ADCADC���ɣ�
��3�����жϳ���FBE=FBE=��GECGEC�������ó���BFEBFE�ס�EGC���ó�![]() �����жϳ�FE=2EG�����ɵó����ۣ�
�����жϳ�FE=2EG�����ɵó����ۣ�
�����������1��DE��
�ʴ�Ϊ��DE��
��2��֤������EF��AB������ΪF��
����BFE=��DFE=90���T��A�T��CDE��
�ߡ�ADC+��CDE=��ADE=��DFE+��FED��
���ADC=��FED��
�ߡ�BFE=90�㣬��B=30�㣬
��BE=2FE��
��BE=2AD��
��FE=AD��
����FED����ADC��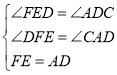
���FED�ա�ADC��
��DE=CD
��3����ͼ3��
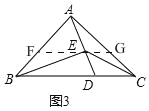
����E��BC��ƽ���ߣ���AB��AC�ֱ��ཻ�ڵ�F��G��
��AB=AC����BAC=90�㣬
���ABC=��ACB=45�㣮
��FG��BC��
���AFG=��ABC=��ACB=��AGF=45�㣬��BFE=135��=��EGC��
��AF=AG��BF=GC��
�ߡ�GEC+��CEB=��GEB=��EFB+��FBE��
���FBE=��GEC
���BFE�ס�EGC��
��![]() ��
��
��FG��BC��
���AFE�ס�ABD����AFG�ס�ADC��
��![]() ��
��![]()
��![]()
��BD=2DC��
��FE=2EG��
��![]() ��
��
��![]() ��
��
��![]()