题目内容
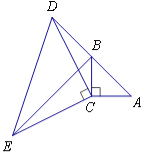
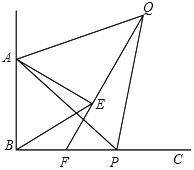
【题目】如图,![]() ,P为射线BC上任意一点
,P为射线BC上任意一点![]() 点P和点B不重合
点P和点B不重合![]() ,分别以AB,AP为边在
,分别以AB,AP为边在![]() 内部作等边
内部作等边![]() 和等边
和等边![]() ,连结QE并延长交BP于点F,连接EP,若
,连结QE并延长交BP于点F,连接EP,若![]() ,
,![]() ,则
,则![]() ______.
______.
【答案】![]()
【解析】
连接EP,过点E作![]() ,由题意可得△AQE≌△ABP,可得QE=BP,
,由题意可得△AQE≌△ABP,可得QE=BP,![]() ,可求
,可求![]() ,根据勾股定理可求
,根据勾股定理可求![]() , BM=
, BM=![]() EM,EF=BF=2FM,EM=
EM,EF=BF=2FM,EM=![]() FM,可求BF=EF=4,EM=2
FM,可求BF=EF=4,EM=2![]() ,FM=2,由QF=11,EF=4,可得BP=EQ=7,可求MP的长,根据勾股定理可求EP的长.
,FM=2,由QF=11,EF=4,可得BP=EQ=7,可求MP的长,根据勾股定理可求EP的长.
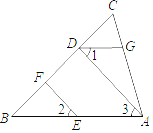
解:如图:连接EP,过点E作![]() .
.
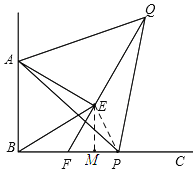
∵△AEB,△APQ是等边三角形
∴ AB=AE=BE=4![]() ,AQ=AP,∠ABE=∠BAE=∠QAP=60°=∠AEB,
,AQ=AP,∠ABE=∠BAE=∠QAP=60°=∠AEB,
∴∠BAP=∠EAQ,且AP=AQ,AB=AE,
∴ △ABP≌△AEQ,
∴EQ=BP,∠AEQ=∠ABC=90°,
∴∠BEF=∠EBF=30°,
∴BF=EF,∠EFM=60°,
∵![]() ,
,
∴∠FEM=30°,
∴EF=2FM =BF,EM=![]() FM,
FM,
∵∠EBM=30°,![]() ,
,
∴BE=2EM,BM=![]() EM,
EM,
∵EB=4![]() ,
,
∴EM=2![]() ,BM=6,
,BM=6,
∵BF+FM=BM,
∴FM=2,BF=EF=4,
∵QF=EF+EF,
∴EQ=11-4=7,
∴ BP=7,
∴MP=BP –BM =1,
在Rt△EMP中,![]() .
.
故答案为:![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】王师傅非常喜欢自驾游,为了解他新买的轿车的耗油情况,将油箱加满后进行了耗油实验,得到下表中的数据:
轿车行驶的路程 | 0 | 100 | 200 | 300 | 400 |
油箱中的剩余油量 | 50 | 42 | 34 | 26 | 18 |
(1)在这个问题中,自变量是 ,因变量是 ;
(2)该轿车油箱的容量为 ![]() ,行驶
,行驶![]() 时,估计油箱中的剩余油量为
时,估计油箱中的剩余油量为 ![]() ;
;
(3)王师傅将油箱加满后,驾驶该轿车从![]() 地前往
地前往![]() 地,到达
地,到达![]() 地时油箱中的剩余油量为
地时油箱中的剩余油量为![]() ,请直接写出
,请直接写出![]() 两地之间的距离是
两地之间的距离是 ![]() .
.