Question

如图，抛物线y=-

1

2

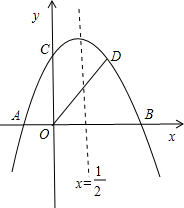x2+bx+c与x轴交于A、B两点（A点在B点左侧），与y轴交于点C，对称轴为直线x=

1

2

，OA=2，OD平分∠BOC交抛物线于点D（点D在第一象限）．
（1）求抛物线的解析式和点D的坐标；
（2）在抛物线的对称轴上，是否存在一点P，使得△BPD的周长最小？若存在，请求出点P的坐标；若不存在，请说明理由．
（3）点M是抛物线上的动点，在x轴上是否存在点N，使A、D、M、N四个点为顶点的四边形是平行四边形？如果存在，求出所有满足条件的M点坐标；如果不存在，请说明理由．

Answer 1

分析：（1）由于A、B关于抛物线的对称轴对称，根据对称轴方程即可求出B点的坐标，然后将它们代入抛物线的解析式中即可求出待定系数的值；OD平分∠BOC，那么直线OD的解析式为y=x，联立抛物线的解析式即可求出D点的坐标；
（2）由于BD的长为定值，若△BPD的周长最短，那么PB+PD应该最短，由于A、B关于抛物线的对称轴对称，连接AD，直线AD与对称轴的交点即为所求的P点，可用待定系数法求出直线AD的解析式，联立抛物线对称轴方程即可得到P点坐标；
（3）此题要分两种情况讨论：
①以AD为对角线的平行四边形AMDN，此时MD∥x轴，则M、D的纵坐标相同，由此可求得M点的坐标；
②以AD为边的平行四边形ADNM，由于平行四边形是中心对称图形，可求得△ADM≌△ADN，即M、N纵坐标的绝对值相等，可据此求出M点的坐标．

解答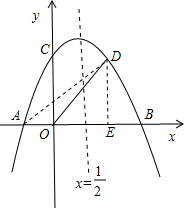：解：（1）∵OA=2
∴A（-2，0）
∵A与B关于直线x=

1

2

对称
∴B（3，0），
由于A、B，两点在抛物线上，
∴

-2-2b+c=0 - 9 2 +3b+C=0

；
解得

b= 1 2 c=3

；
∴y=-

1

2

x2+

1

2

x+3
过D作DE⊥x轴于E
∵∠BOC=90°，OD平分∠BOC
∴∠DOB=45°，∠ODE=45°，
∴DE=OE
即x_D=y_D，
∴x=-

1

2

x2+

1

2

x+3，
解得x₁=2，x₂=-3（舍去）
∴D（2，2）；（4分）

（2）存在
∵BD为定值，
∴要使△BPD的周长最小，只需PD+PB最小
∵A与B关于直线x=

1

2

对称，
∴PB=PA，只需PD+PA最小
∴连接AD，交对称轴于点P，此时PD+PA最小，（2分）
由A（-2，0），D（2，2）可得
直线AD：y=

1

2

x+1（1分）
令x=

1

2

，y=

5

4

∴存在点P(

1

2

，

5

4

)，使△BPD的周长最小（1分）

（3）存在．
（i）当AD为平行四边形AMDN的对角线时，MD∥AN，即MD∥x轴
∴y_M=y_D，
∴M与D关于直线x=

1

2

对称，
∴M（-1，2）（1分）
（ii）当AD为平行四边形ADNM的边时，
∵平行四边形ADNM是中心对称图形，△AND≌△ANM
∴|y_M|=|y_D|，
即y_M=-y_D=-2，
∴令-

1

2

x2+

1

2

x+3=-2，即x²-x-10=0；
解得x1，2=

1± 41

2

，M(

1+ 41

2

，-2)或M(

1- 41

2

，-2)，（2分）
综上所述：满足条件的M点有三个M（-1，2），M(

1+ 41

2

，-2)或M(

1- 41

2

，-2）．（1分）

点评：此题主要考查了二次函数解析式的确定、轴对称的性质、平行四边形的判定和性质等，需注意的是（3）题在不确定平行四边形边和对角线的情况下需要分类讨论，以免漏解．