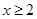题目内容
(2011•重庆)如图,在平面直角坐标系x0y中,一次函数y=kx+b(k≠0)的图象与反比例函数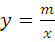 (m≠0)的图象交于二、四象限内的A、B两点,与x轴交于C点,点B的坐标为(6,n).线段OA=5,E为x轴上一点,且sin∠AOE=
(m≠0)的图象交于二、四象限内的A、B两点,与x轴交于C点,点B的坐标为(6,n).线段OA=5,E为x轴上一点,且sin∠AOE=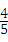 .
.
(1)求该反比例函数和一次函数的解析式;
(2)求△AOC的面积.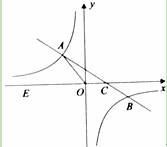
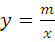 (m≠0)的图象交于二、四象限内的A、B两点,与x轴交于C点,点B的坐标为(6,n).线段OA=5,E为x轴上一点,且sin∠AOE=
(m≠0)的图象交于二、四象限内的A、B两点,与x轴交于C点,点B的坐标为(6,n).线段OA=5,E为x轴上一点,且sin∠AOE=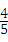 .
.(1)求该反比例函数和一次函数的解析式;
(2)求△AOC的面积.

解:(1)过点A作AD⊥x轴于D点,如图

∵sin∠AOE=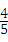 ,OA=5,
,OA=5,
∴sin∠AOE=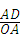 =
=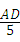 =
=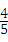 ,
,
∴AD=4,
∴DO=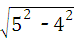 =3,
=3,
而点A在第二象限,
∴点A的坐标为(﹣3,4),
将A(﹣3,4)代入y=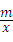 ,得m=﹣12,
,得m=﹣12,
∴反比例函数的解析式为y=﹣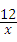 ;
;
将B(6,n)代入y=﹣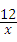 ,得n=﹣2;
,得n=﹣2;
将A(﹣3,4)和B(6,﹣2)分别代入y=kx+b(k≠0),得
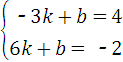 ,
,
解得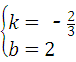 ,
,
∴所求的一次函数的解析式为y=﹣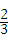 x+2;
x+2;
(2)在y=﹣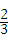 x+2中,令y=0,
x+2中,令y=0,
即﹣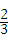 x+2=0,
x+2=0,
解得x=3,
∴C点坐标为(0,3),即OC=3,
∴S△AOC=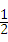 •AD•OC=
•AD•OC=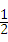 •4•3=6.
•4•3=6.

∵sin∠AOE=
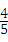 ,OA=5,
,OA=5,∴sin∠AOE=
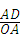 =
=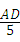 =
=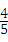 ,
,∴AD=4,
∴DO=
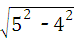 =3,
=3,而点A在第二象限,
∴点A的坐标为(﹣3,4),
将A(﹣3,4)代入y=
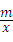 ,得m=﹣12,
,得m=﹣12,∴反比例函数的解析式为y=﹣
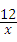 ;
;将B(6,n)代入y=﹣
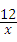 ,得n=﹣2;
,得n=﹣2;将A(﹣3,4)和B(6,﹣2)分别代入y=kx+b(k≠0),得
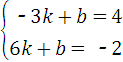 ,
,解得
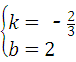 ,
,∴所求的一次函数的解析式为y=﹣
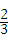 x+2;
x+2;(2)在y=﹣
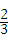 x+2中,令y=0,
x+2中,令y=0,即﹣
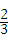 x+2=0,
x+2=0,解得x=3,
∴C点坐标为(0,3),即OC=3,
∴S△AOC=
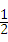 •AD•OC=
•AD•OC=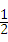 •4•3=6.
•4•3=6.略

练习册系列答案
相关题目

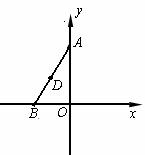
 .在x轴上取一点P,过点P作直线OA的垂线l,以直线l为对称轴,线段OB经轴对称变换后的像是O´B´.
.在x轴上取一点P,过点P作直线OA的垂线l,以直线l为对称轴,线段OB经轴对称变换后的像是O´B´.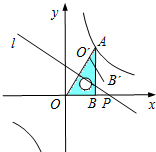
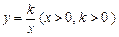 的图象经过点A(1, 2),B(m ,n)(m>1),过点B作y轴的垂线,垂足为C.
的图象经过点A(1, 2),B(m ,n)(m>1),过点B作y轴的垂线,垂足为C.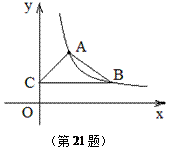
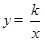 和
和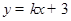 的图象大致是
的图象大致是 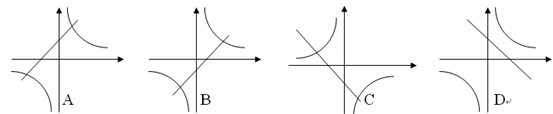
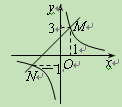
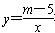 在第一象限内相交于点M,与x轴交于点A.
在第一象限内相交于点M,与x轴交于点A. (2)若点B的坐标为(3,0),AM=5,S△ABM=8,求双曲线的函数表达式.
(2)若点B的坐标为(3,0),AM=5,S△ABM=8,求双曲线的函数表达式.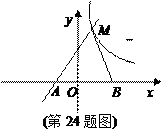
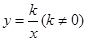 的图象如图所示,若点A(
的图象如图所示,若点A(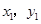 )、B(
)、B(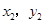 )、C(
)、C(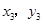 )是这个函数图象上的三点,且
)是这个函数图象上的三点,且 ,则
,则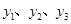 的大小关系( )
的大小关系( )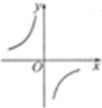
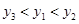
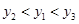
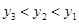
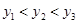
 的自变量
的自变量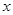 的取值范围是
的取值范围是