题目内容
(2011?金华)如图,将一块直角三角板OAB放在平面直角坐标系中,B(2,0),∠AOB=60°,点A在第一象限,过点A的双曲线为 .在x轴上取一点P,过点P作直线OA的垂线l,以直线l为对称轴,线段OB经轴对称变换后的像是O´B´.
.在x轴上取一点P,过点P作直线OA的垂线l,以直线l为对称轴,线段OB经轴对称变换后的像是O´B´.
当点O´与点A重合时,点P的坐标是___________
设P(t,0),当O´B´与双曲线有交点时,t的取值范围是______________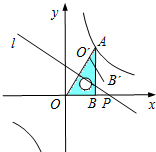
 .在x轴上取一点P,过点P作直线OA的垂线l,以直线l为对称轴,线段OB经轴对称变换后的像是O´B´.
.在x轴上取一点P,过点P作直线OA的垂线l,以直线l为对称轴,线段OB经轴对称变换后的像是O´B´.当点O´与点A重合时,点P的坐标是___________
设P(t,0),当O´B´与双曲线有交点时,t的取值范围是______________

(4,0) 4≤t≤2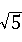 或﹣2
或﹣2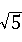 ≤t≤4.
≤t≤4.
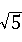 或﹣2
或﹣2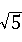 ≤t≤4.
≤t≤4.(1)当点O´与点A重合时,
∵∠AOB=60°,过点P作直线OA的垂线l,以直线l为对称轴,线段OB经轴对称变换后的像是O´B´.
AP′=OP′,
∴△AOP′是等边三角形,
∵B(2,0),
∴BO=BP′=2,
∴点P的坐标是(4,0),
(2)∵∠AOB=60°,∠P′MO=90°,
∴∠MP′O=30°,
∴OM= t,OO′=t,
t,OO′=t,
过O′作O′N⊥X轴于N,
∠OO′N=30°,
∴ON= t,NO′=
t,NO′=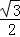 t,
t,
∴O′( t,
t,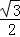 t),
t),
根据对称性可知点P在直线O′B′上,
设直线O′B′的解析式是y=kx+b,代入得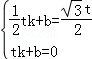 ,
,
解得: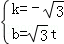 ,
,
∴y=﹣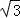 x+
x+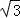 t①,
t①,
∵∠ABO=90°,∠AOB=60°,OB=2,
∴OA=4,AB=2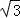 ,
,
∴A(2,2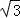 )),代入反比例函数的解析式得:k=4
)),代入反比例函数的解析式得:k=4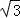 ,
,
∴y=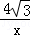 ②,
②,
①②联立得,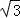 x2﹣
x2﹣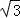 tx+4
tx+4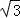 =0,
=0,
即x2﹣tx+4=0③,
b2﹣4ac=t2﹣4×1×4≥0,
解得:t≥4,t≤﹣4.
又O′B′=2,根据对称性得B′点横坐标是1+ t,
t,
当点B′为直线与双曲线的交点时,
由③得,(x﹣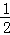 t)2﹣
t)2﹣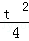 +4=0,
+4=0,
代入,得(1+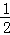 t﹣
t﹣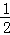 t)2﹣
t)2﹣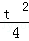 +4=0,
+4=0,
解得t=±2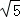 ,
,
而当线段O′B′与双曲线有交点时,
t≤2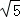 或t≥﹣2
或t≥﹣2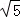 ,
,
综上所述,t的取值范围是4≤t≤2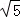 或﹣2
或﹣2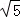 ≤t≤﹣4.
≤t≤﹣4.

∵∠AOB=60°,过点P作直线OA的垂线l,以直线l为对称轴,线段OB经轴对称变换后的像是O´B´.
AP′=OP′,
∴△AOP′是等边三角形,
∵B(2,0),
∴BO=BP′=2,
∴点P的坐标是(4,0),
(2)∵∠AOB=60°,∠P′MO=90°,
∴∠MP′O=30°,
∴OM=
 t,OO′=t,
t,OO′=t,过O′作O′N⊥X轴于N,
∠OO′N=30°,
∴ON=
 t,NO′=
t,NO′=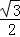 t,
t,∴O′(
 t,
t,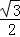 t),
t),根据对称性可知点P在直线O′B′上,
设直线O′B′的解析式是y=kx+b,代入得
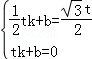 ,
,解得:
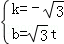 ,
,∴y=﹣
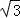 x+
x+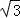 t①,
t①,∵∠ABO=90°,∠AOB=60°,OB=2,
∴OA=4,AB=2
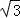 ,
,∴A(2,2
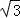 )),代入反比例函数的解析式得:k=4
)),代入反比例函数的解析式得:k=4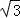 ,
,∴y=
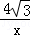 ②,
②,①②联立得,
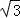 x2﹣
x2﹣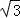 tx+4
tx+4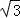 =0,
=0,即x2﹣tx+4=0③,
b2﹣4ac=t2﹣4×1×4≥0,
解得:t≥4,t≤﹣4.
又O′B′=2,根据对称性得B′点横坐标是1+
 t,
t,当点B′为直线与双曲线的交点时,
由③得,(x﹣
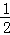 t)2﹣
t)2﹣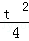 +4=0,
+4=0,代入,得(1+
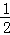 t﹣
t﹣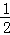 t)2﹣
t)2﹣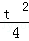 +4=0,
+4=0,解得t=±2
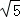 ,
,而当线段O′B′与双曲线有交点时,
t≤2
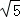 或t≥﹣2
或t≥﹣2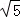 ,
,综上所述,t的取值范围是4≤t≤2
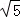 或﹣2
或﹣2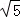 ≤t≤﹣4.
≤t≤﹣4.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
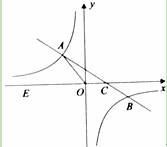
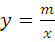 (m≠0)的图象交于二、四象限内的A、B两点,与x轴交于C点,点B的坐标为(6,n).线段OA=5,E为x轴上一点,且sin∠AOE=
(m≠0)的图象交于二、四象限内的A、B两点,与x轴交于C点,点B的坐标为(6,n).线段OA=5,E为x轴上一点,且sin∠AOE=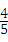 .
.
 中自变量x的取值范围是 .
中自变量x的取值范围是 . 的图象经过点(2,-3),则
的图象经过点(2,-3),则 =
= 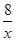 的图象交于点A、点B,点A的坐标为(2,4),则点B的坐标是 。
的图象交于点A、点B,点A的坐标为(2,4),则点B的坐标是 。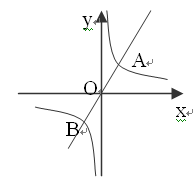
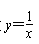 的图象的对称轴有_ ▲ 条.
的图象的对称轴有_ ▲ 条. (k是常数,k≠0)的图像经过点(-1,2),那么这个函数的解析式是__________.
(k是常数,k≠0)的图像经过点(-1,2),那么这个函数的解析式是__________.  以加热的饮水机,该饮水机的工作程序是:放满水后,
以加热的饮水机,该饮水机的工作程序是:放满水后,
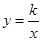 上,则下列点一定在该曲线上的是( )
上,则下列点一定在该曲线上的是( )