Question

【题目】如图，△ABC中，⊙O是△ABC的内切圆，切点分别为D、E、F．

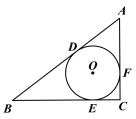
（1）已知∠C＝90°．

①若BD＝6，AD＝4，则⊙O的半径r为 ，△ABC的面积为 ；

②若BD＝m，AD＝n，请用含m、n的代数式表示△ABC的面积；

（2）若，试判断△ABC的形状，并说明理由。

Answer 1

【答案】（1）①2；24；②mn ；（2）直角三角形，理由见解析.

【解析】

（1）①先根据切线长定理得出，再根据勾股定理列出关于的方程，解方程即可，再根据三角形面积公式求解即可；

②根据①中的式子代入，利用完全平方公式和平方差公式得出，然后根据三角形面积公式求解即可；

（2）先把转化成，然后对变形整理得到结果为，即可证明是直角三角形.

（1）①连接OD、OE、OF，如图所示：

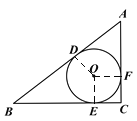
∵是的内切圆，D、E、F为切点，

∴，

又∵，

∴四边形ECFO为正方形，

∴，

∴，

∴，

解得：或（舍去），

∴；

②∵，

由①可知，

对上式右边进行配方得：，

∴，

∴；

（2）∵，

∴

，

∴是直角三角形.