题目内容
【题目】如图所示,在△ABC中,∠BAC=90°,AD⊥BC于D,BF平分∠ABC,交AD于E,若AE=13,求AF的长度.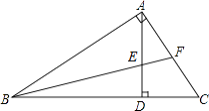
【答案】解:∵∠BAC=90°,
∴∠ABF+∠AFB=90°,
又∵AD⊥BC,
∴∠ADB=90°,
∴∠EBD+∠BED=90°,
又∵BF平分∠ABC,
∴∠ABF=∠EBD,
∴∠AFB=∠BED,
又∵∠AEF=∠BED,
∴∠AEF=∠AFB,
∴AE=AF,
∵AE=13,
∴AF=13.
【解析】根据三角形内角和定理和角平分线性质得到∠AEF=∠AFB,根据等角对等边得到AE=AF,求出AF的长度.
【考点精析】认真审题,首先需要了解三角形的内角和外角(三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目