题目内容
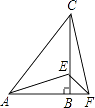
【题目】如图，某沿海开放城市A接到台风警报，在该市正南方向100km的B处有一台风中心，沿BC方向以20km/h的速度向D移动，已知城市A到BC的距离AD=60km，那么台风中心经过多长时间从B点移到D点？如果在距台风中心30km的圆形区域内都将有受到台风的破坏的危险，正在D点休闲的游人在接到台风警报后的几小时内撤离才可脱离危险？
【答案】解：∵AB=100km，AD=60km，
∴在Rt△ABD中，根据勾股定理，得BD= 
=80km，
则台风中心经过80÷20=4小时从B移动到D点；
如图，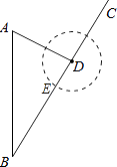 
∵距台风中心30km的圆形区域内都会受到不同程度的影响，
∴人们要在台风中心到达E点之前撤离，
∵BE=BD﹣DE=80﹣30=50km，
∴游人在 
=2.5小时内撤离才可脱离危险．
【解析】由题意根据勾股定理求出BD的值，由沿BC方向以20km/h的速度向D移动，求出台风中心经过几个小时从B移动到D点；由距台风中心30km的圆形区域内都会受到不同程度的影响，得到人们要在台风中心到达E点之前撤离，求出撤离的时间.
练习册系列答案
相关题目
