题目内容
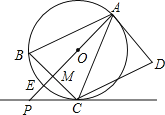
【题目】如图，AD是
的切线，切点为A，AB是的弦，过点B作
，交于点C，连接AC，过点C作
，交AD于点D，连接AO并延长AO交BC于点M，交
于点E，交过点C的直线于点P，且
．
求证：
；
判断直线PC与的位置关系，并说明理由；
若
，
，求PC的长．
【答案】（1）证明见解析；（2）
与圆O相切，理由见解析.（3）
【解析】分析：（1）由AD是⊙O的切线，BC∥AD，易得AO⊥BC，然后由垂径定理求得
，继而证得结论；
（2）过C点作直径CF，连接FB，由CF为直径得∠F+∠BCE=90°，由AB∥DC得∠ACD=∠BAC，而∠BAC=∠F，∠BCP=∠ACD，所以∠F=∠BCP，于是∠BCP+∠BCF=90°，然后根据切线的判断得到结论；
（3）根据切线的性质得到OA⊥AD，而BC∥AD，则AM⊥BC，根据垂径定理求得BM与CM的长，根据等腰三角形性质有AC=AB=9，在Rt△AMC中根据勾股定理计算出AM=6
，设⊙O的半径为r，则OC=r，OM=AM-r=6-r，在Rt△OCM中，根据勾股定理计算出r的值即可．
详解：
证明：
是
的切线，
，
，
，
，
；
与圆O相切，理由为：
解：过C点作直径CF，连接FB，如图，
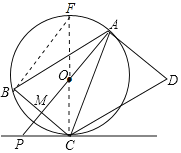
为直径，
，即
，
，
，
，
．
，
，即
，
，
与圆O相切；
解：是的切线，切点为A
，
，
，
，
，
在
中，
，
设的半径为r，则
，
，
在
中，
，即
，
解得：
，
，
，
，
，
∽
，
：
：FB，
，
．
练习册系列答案
相关题目
【题目】如图，有一个形如六边形的点阵，它的中心是一个点，算做第一层，第二层每边两个点，第三层每边三个点，以此类推．
（1）填写下表：
层数 |
|
|
|
|
|
该层对应的点数 |
|
|
| ________ | ________ |
（2）写出第
层对应的点数（
）；
