题目内容
在直角坐标系中，已知O（0，0），A（2，0），B（0，4），C（0，3），D为x轴上一点．若以D、O、C为顶点的三角形与△AOB相似，这样的D点有（ ）
| A、3个 | B、4个 | C、5个 | D、6个 |
分析：由相似三角形对应边成比例且夹角相等的三角形相似，分别从若△OCD∽△OBA与若△OCD∽△OAB去分析即可求得答案．
解答：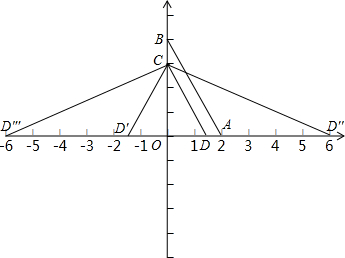
解：如图：
若△OCD∽△OBA，
则需
=
，
∴
=
，
∴OD=
，
∴D与D′的坐标分别为（
，0），（-
，0），
若△OCD∽△OAB，
则需
=
，
即
=
，
∴OD=6，
∴D″与D′″的坐标分别为（6，0），（-6，0）．
∴若以D、O、C为顶点的三角形与△AOB相似，这样的D点有4个．
故选B．
解：如图：若△OCD∽△OBA，
则需
| OC |
| OB |
| OD |
| OA |
∴
| 3 |
| 4 |
| OD |
| 2 |
∴OD=
| 3 |
| 2 |
∴D与D′的坐标分别为（
| 3 |
| 2 |
| 3 |
| 2 |
若△OCD∽△OAB，
则需
| OC |
| OA |
| OD |
| OB |
即
| 3 |
| 2 |
| OD |
| 4 |
∴OD=6，
∴D″与D′″的坐标分别为（6，0），（-6，0）．
∴若以D、O、C为顶点的三角形与△AOB相似，这样的D点有4个．
故选B．
点评：此题考查了相似三角形的判定与性质．注意分类讨论思想与数形结合思想的应用是解此题的关键．
练习册系列答案
相关题目
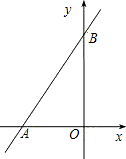如图，在直角坐标系中，已知直线y=kx+6与x轴、y轴分别交于A、B两点，且△ABO的面积为12．
的直角顶点的坐标为