题目内容
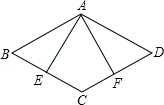
如图,四边形ABCD为等腰梯形,AD∥BC,连结AC、BD.在平面内将△DBC沿BC翻折得到△EBC.

(1)四边形ABEC一定是什么四边形?
(2)证明你在(1)中所得出的结论.

(1)四边形ABEC一定是什么四边形?
(2)证明你在(1)中所得出的结论.
解:(1)四边形ABEC一定是平行四边形。
(2)证明:∵四边形ABCD为等腰梯形,AD∥BC,∴AB=DC,AC=BD。
由折叠的性质可得:EC=DC,DB=BE,
∴EC=AB,BE=AC。
∴四边形ABEC是平行四边形。
(2)证明:∵四边形ABCD为等腰梯形,AD∥BC,∴AB=DC,AC=BD。
由折叠的性质可得:EC=DC,DB=BE,
∴EC=AB,BE=AC。
∴四边形ABEC是平行四边形。
试题分析:(1)首先观察图形,然后由题意可得四边形ABEC一定是平行四边形。
(2)由四边形ABCD为等腰梯形,AD∥BC,可得AB=DC,AC=BD,又由在平面内将△DBC沿BC翻折得到△EBC,可得EC=DC,DB=BE,继而可得:EC=AB,BE=AC,则可证得四边形ABEC是平行四边形。

练习册系列答案
相关题目