题目内容
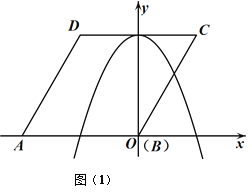
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,⊙
,⊙![]() 与
与![]() 、
、![]() 、
、![]() 都相切,切点分别是
都相切,切点分别是![]() 、
、![]() 、
、![]() ,
,![]() 、
、![]() 的延长线交于点
的延长线交于点![]() ,
,![]() 、
、![]() 是关于
是关于![]() 的方程
的方程![]() 的两个根.
的两个根.
(1)求证:![]() 是直角三角形;
是直角三角形;
(2)若![]() ,求四边形CEDF的面积.
,求四边形CEDF的面积.
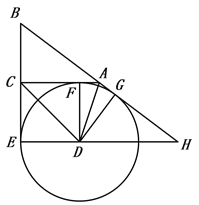
【答案】(1)证明见解析(2)36
【解析】分析:(1)根据根与系数的关系证明![]() ;(2)判断四边形CEDF是正方形,根据
;(2)判断四边形CEDF是正方形,根据![]() ,列方程求正方形的边长.
,列方程求正方形的边长.
详解:(1)证明:∵![]() 是关于
是关于![]() 的方程
的方程![]() 的两个根,
的两个根,
∴![]() ,
,![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
∴△ABC是直角三角形;
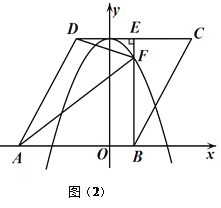
(2)解:连DB,如图
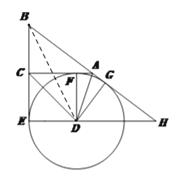
∵![]() ,即
,即![]() ,
,
又∵在![]() 中,
中,![]() ,
,
∴![]() ,得
,得![]() ,
,
设![]() ,则
,则![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,解得
,解得![]() ,
,
∴![]() ,
,![]() ,
,![]() .
.
∵⊙D与BC,AC,AB都相切,切点分别是E,F,G,
∴DE=DF=DG,DE⊥BC,DG⊥AB,
∴四边形DECF为正方形,
设DE=DF=DG=![]() ,则BE=
,则BE=![]() ,BH=
,BH=![]() ,EH=
,EH=![]() ,
,
∵![]() ,
,
∴![]() ,解得
,解得![]() ,
,
∴![]() .
.

练习册系列答案
相关题目