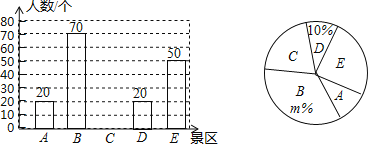
题目内容
【题目】如图,直线:y=﹣![]() +4与x轴、y轴分别別交于点M、点N,等边△ABC的高为3,边BC在x轴上,将△ABC沿着x轴的正方向平移,在平移过程中,得到△A1B1C1,当点B1与原点O重合时,解答下列问题:
+4与x轴、y轴分别別交于点M、点N,等边△ABC的高为3,边BC在x轴上,将△ABC沿着x轴的正方向平移,在平移过程中,得到△A1B1C1,当点B1与原点O重合时,解答下列问题:
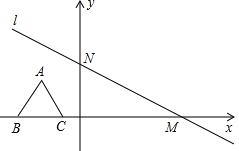
(1)点A1的坐标为 .
(2)求△A1B1C1的边A1C1所在直线的解析式;
(3)若以P、A1、C1、M为顶点的四边形是平行四边形,请直接写出P点坐标.
【答案】(1)(![]() ,3);(2)y=﹣
,3);(2)y=﹣![]() x+6;(3)点P的坐标为:(3
x+6;(3)点P的坐标为:(3![]() ,3)或(5
,3)或(5![]() ,﹣3)或(﹣
,﹣3)或(﹣![]() ,3)
,3)
【解析】
(1)当点B1与原点O重合时,过点A1作A1D⊥x轴于点D,则A1D=3,则B1D=A1Dtan30°=3×![]() =
=![]() ,当x=
,当x=![]() 时,y=﹣
时,y=﹣![]() +4=3=A1D,故点A1在直线上,点A1(
+4=3=A1D,故点A1在直线上,点A1(![]() ,3);
,3);
(2)将点C1(![]() ,0)、A1的坐标代入一次函数表达式y=kx+b,即可求解;
,0)、A1的坐标代入一次函数表达式y=kx+b,即可求解;
(3)分A1C1是平行四边形的边、A1C1是平行四边形的对角线两种情况,分别求解即可.
解:(1)直线:y=﹣![]() +4与x轴、y轴分别別交于点M、点N,
+4与x轴、y轴分别別交于点M、点N,
则点M(4![]() ,0),
,0),
当点B1与原点O重合时,过点A1作A1D⊥x轴于点D,
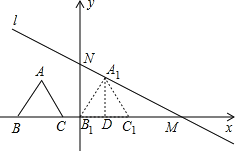
则A1D=3,则B1D=A1Dtan30°=3×![]() =
=![]() ,
,
当x=![]() 时,y=﹣
时,y=﹣![]() +4=3=A1D,故点A1在直线上,
+4=3=A1D,故点A1在直线上,
点A1(![]() ,3),故答案为:(
,3),故答案为:(![]() ,3);
,3);
(2)将点C1(![]() ,0)、A1的坐标代入一次函数表达式:y=kx+b
,0)、A1的坐标代入一次函数表达式:y=kx+b
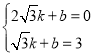
并解得: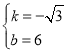
直线A1C1的表达式为:y=﹣![]() x+6;
x+6;
(3)设点P(m,n)
①当A1C1是平行四边形的边时,
则![]() ,0﹣3=n或
,0﹣3=n或![]() ,0+3=n
,0+3=n
解得:m=![]() 或
或![]() ,n=3或﹣3,
,n=3或﹣3,
故点P的坐标为:(![]() ,3)或(
,3)或(![]() ,﹣3);
,﹣3);
②当A1C1是平行四边形的对角线时,
由中点公式得:![]()
解得:m=![]() ,n=3,故点P(
,n=3,故点P(![]() ,3);
,3);
综上点P的坐标为:(3![]() ,3)或(5
,3)或(5![]() ,﹣3)或(﹣
,﹣3)或(﹣![]() ,3).
,3).