题目内容

【题目】如图，在正方形ABCD中，对角线AC，BD交于点0，过点0的直线分别交边AD，BC于点E，F，EF=6．则AE2+BF2的值为（ ）

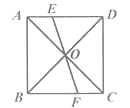
A. 9 B. 16 C. 18 D. 36

【答案】C

【解析】过点A作AM∥EF交BC于点M，易证四边形AEFM是平行四边形，可得出AM=EF，AE=MF，再通过证三角形全等，得出AE=CF，可得出BA2=BF2+2BFAE+AE2（1），再在Rt△ABM中，利用勾股定理得出MA2=AB2+BF2-2BFAE+AE2（2），然后由（1）+（2），可求出结果.

过点A作AM∥EF交BC于点M

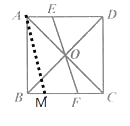
∵正方形ABCD

∴AD∥BC，OA=OC

∠EAO=∠FCO

在△AOE和△COF中

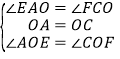
∴△AOE≌△COF（ASA）

∴AE=CF

∴BC=BF+FC

BA2=BC2=(BF+AE）2,

即BA2=BF2+2BFAE+AE2（1）

∵AD∥BC，AM∥EF

∴四边形AEFM是平行四边形

∴AE=MF，AM=EF=6

∴BM=BF-MF=BF-AE

在Rt△ABM中

MA2=AB2+(BF-AE）2=AB2+BF2-2BFAE+AE2（2）

由（1）+（2）得

BA2+EF2=BF2+2BFAE+AE2+AB2+BF2-2BFAE+AE2

36=2BF2+2AE2

∴AE2+BF2=18

故选：C.

练习册系列答案
相关题目

【题目】汽车超速行驶是交通安全的重大隐患，为了有效降低交通事故的发生，许多道路在事故易发路段设置了区间测速如图，学校附近有一条笔直的公路l，其间设有区间测速，所有车辆限速40千米/小时数学实践活动小组设计了如下活动：在l上确定A，B两点，并在AB路段进行区间测速．在l外取一点P，作PC⊥l，垂足为点C．测得PC=30米，∠APC=71°，∠BPC=35°．上午9时测得一汽车从点A到点B用时6秒，请你用所学的数学知识说明该车是否超速．（参考数据：sin35°≈0.57，cos35°≈0.82，tan35°≈0.70，sin71°≈0.95，cos71°≈0.33，tan71°≈2.90）

【题目】随州市新水一桥（如图1）设计灵感来源于市花﹣﹣兰花，采用蝴蝶兰斜拉桥方案，设计长度为258米，宽32米，为双向六车道，2018年4月3日通车．斜拉桥又称斜张桥，主要由索塔、主梁、斜拉索组成．某座斜拉桥的部分截面图如图2所示，索塔AB和斜拉索（图中只画出最短的斜拉索DE和最长的斜拉索AC）均在同一水平面内，BC在水平桥面上．已知∠ABC=∠DEB=45°，∠ACB=30°，BE=6米，AB=5BD．

（1）求最短的斜拉索DE的长；

（2）求最长的斜拉索AC的长．

【题目】已知，如图，在△ABC中，OB和OC分别平分∠ABC和∠ACB，过O作DE∥BC，分别交AB、AC于点D、E，若DE=8，则线段BD+CE的长为

A. 5B. 6C. 7D. 8

【题目】如图所示，将二次函数y=x2+2x+1的图象沿x轴翻折，然后向右平移1个单位，再向上平移4个单位，得到二次函数y=ax2+bx+c的图象．函数y=x2+2x+1的图象的顶点为点A．函数y=ax2+bx+c的图象的顶点为点B，和x轴的交点为点C，D（点D位于点C的左侧）．

（1）求函数y=ax2+bx+c的解析式；

（2）从点A，C，D三个点中任取两个点和点B构造三角形，求构造的三角形是等腰三角形的概率；

（3）若点M是线段BC上的动点，点N是△ABC三边上的动点，是否存在以AM为斜边的Rt△AMN，使△AMN的面积为△ABC面积的？若存在，求tan∠MAN的值；若不存在，请说明理由．

【题目】如图，已知△ABC中，AB=6cm，∠B=∠C，BC=4cm，点D为AB的中点．若点P在线段BC上以1cm/s的速度由点B向点C运动，同时，点Q在线段CA上由点C向点A运动．

（1）若点Q的运动速度与点P的运动速度相等，经过1秒后，△BPD与△CQP是否全等，请说明理由；

（2）若点Q的运动速度与点P的运动速度不相等，当点Q的运动速度为多少时，能够使△BPD与△CQP全等？

【题目】把下列各数填入相应的大括号内．

3，－，，0．5，2π，3．14159265，－，1．103030030003…(相

邻两个3之间依次多1个0)．

(1) 有理数集合：{ }；

(2) 无理数集合：{ }；

(3) 实数集合：{ }；

(4) 负实数集合：{ }．

【题目】一扇窗户如图1所示，窗框和窗扇用“滑块铰链”连接．如图2是图1中“滑块铰链”的平面示意图，滑轨MN安装在窗框上，托悬臂DE安装在窗扇上，支点4处装有滑块，滑块可以左右滑动，支点B，C,D在一条直线上，延长DE交MN于点F．已知AC=DE=20cm，AE=CD=10cm，BD=40cm．

（1）当∠CAB=35 时，求窗扇与窗框的夹角∠DFB的度数．

（2）当窗扇关闭时，图中点E，A,D，C,B都在滑轨MN上．求此时点A与点B之间的距离．

（3）在(2)的前提下，将窗户推开至四边形ACDE为矩形时，求点A处的滑块移动的距离．

【题目】下表是今年雨季某河流一周的水位变化情况(上周末的水位达到警戒水位)

星期

一

二

三

四

五

六

日

水位记录

注:此河流的警戒水位为米．

完成下面的本周水位变化记录表:

星期

一

二

三

四

五

六

日

水位变化(与前一天比较)

(注:规定水位比前一天上升用“”，水位比前一天下降用“”，不升不降记作“”．)

与上周末相比，本周末河流水位是上升了还是下降了? (填“上升”或“下降”)

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网