Question

【题目】如图，四边形ABCD中，∠B=90°，AB=BC=3 ，CD=8，AD=10．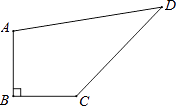
（1）求∠BCD的度数．
（2）求四边形ABCD的面积．

Answer 1

【答案】
（1）解：连接AC，

在Rt△ABC中，∠B=90°，AB=BC=3 ，

根据勾股定理得：AC= =6，∠ACB=45°，

∵CD=8，AD=10，

∴AD2=AC2+CD2，

∴△ACD为直角三角形，即∠ACD=90°，

则∠BCD=∠ACB+∠ACD=135°；

（2）解：根据题意得：S四边形ABCD=S△ABC+S△ACD= ×3 ×3 + ×6×8=9+24=33
【解析】（1）连接AC，在直角三角形ABC中，利用勾股定理求出AC的长，再由CD与AD的长，利用勾股定理的逆定理判断得到三角形ACD为直角三角形，再由等腰直角三角形的性质，根据∠BCD=∠ACB+∠ACD即可求出；（2）四边形ABCD面积=三角形ABC面积+三角形ACD面积，求出即可．
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识，掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2，以及对勾股定理的逆定理的理解，了解如果三角形的三边长a、b、c有下面关系：a2+b2=c2，那么这个三角形是直角三角形．