题目内容
【题目】如图,将边长都为2 ![]() cm的正方形按如图所示摆放,点A1、A2、…、An分别是正方形的中心,则2014个这样的正方形重叠部分的面积和为 .
cm的正方形按如图所示摆放,点A1、A2、…、An分别是正方形的中心,则2014个这样的正方形重叠部分的面积和为 . 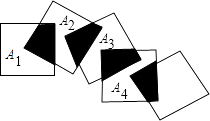
【答案】4026
【解析】解:如图,过点A1作A1D、A1E与正方形的边垂直, 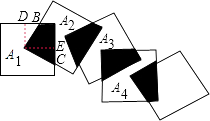
∵A1是正方形的中心,
∴A1D=A1E,A1D⊥A1E,
∵∠BA1D+∠BA1E=∠CA1E+∠BA1E,
∴∠BA1D=∠CA1E,
在△A1BD和△A1CE中,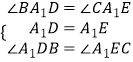 ,
,
∴△A1BD≌△A1CE(SAS),
∴阴影部分的面积=正方形面积的 ![]() =
= ![]() ×(2
×(2 ![]() )2=2,
)2=2,
∴2014个这样的正方形重叠部分的面积和=2×(2014﹣1)=4026.
故答案为:4026.
标注字母,过点A1作A1D、A1E与正方形的边垂直,根据正方形的性质可得A1D=A1E,再求出∠BA1D=∠CA1E,然后利用“角边角”证明△A1BD和△A1CE全等,然后根据全等三角形的性质可得阴影部分的面积等于正方形面积的 ![]() ,再根据重叠部分的个数比正方形的个数少1进行计算即可得解.
,再根据重叠部分的个数比正方形的个数少1进行计算即可得解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目