Question

【题目】如图所示是10×8的网格，网格中每个小正方形的边长均为1，A、B两点在小正方形的顶点上，使以A、B、C为顶点的三角形分别满足以下要求：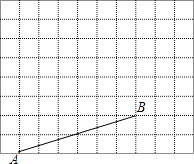
（1）请在图中取一点C（点C必须在小正方形的顶点上），使△ABC为钝角等腰三角形；
（2）通过计算，直接写出△ABC的周长．

Answer 1

【答案】
（1）解：如图所示，△ABC为所求的三角形；

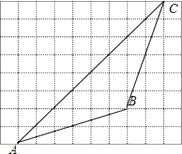
（2）解：由题意得：AB=BC= =2 ，

AC= =8 ，

则△ABC周长为4 +8

【解析】（1）如图所示，使AB=BC，连接AC，得到三角形ABC；（2）在网格中，利用勾股定理分别求出AB，BC以及AC的长，即可确定出三角形ABC周长．
【考点精析】根据题目的已知条件，利用等腰三角形的判定和勾股定理的概念的相关知识可以得到问题的答案，需要掌握如果一个三角形有两个角相等，那么这两个角所对的边也相等（简称：等角对等边）．这个判定定理常用于证明同一个三角形中的边相等；直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2．