��Ŀ����
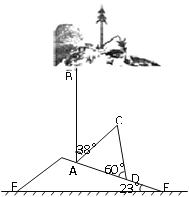
����Ŀ��2011��3��11��13ʱ46���ձ�������9.0������𣬰����ž��Ǻ�Х��ɽ������һ����ˮƽ�洹ֱ�Ĵ����� ��Х������������б���۶ϵ���ɽ���ϣ����Ķ���ǡ�ýӴ������棨��ͼ��ʾ������֪ɽ�µ��½ǡ�AEF=23�㣬�������ɵ���б��Ϊ��BAC=38�㣬�������۶ϲ��ֺ��������ɵĽǡ�ADC=60�㣬AD=4m��
��1�����DAC�Ķ�����
��2������ô����۶�ǰAB�ĸߣ��������ȷ����λ���ο����ݣ� ![]() ����
����
���𰸡���1��75�㡭����5��
��2��10��������10��
�������������������1������ӳ�BA��EF�ڵ�G����ôBG��EF����CAE=180��-��BAC-��EAG����BAC�Ķ����Լ�ȷ����ֻҪ�����GAE���ɣ�ֱ��������GAE����E�Ķ�����֪����ô��EAG�Ķ�������������ˣ���CAE��������
��2�������۶�ǰ�ĸ߶ȣ�������AC��CD�ij����������A��AH��CD������ΪH������CDA=60����ͨ��������ֱ��������AHD��ACH������AD��CD��ֵ��
��1���ӳ�BA��EF�ڵ�G

��Rt��AGE����E=23����
���GAE=67����
���ߡ�BAC=38����
���CAE=180��-67��-38��=75����
��2����AH��CD������ΪH��
��AD=4����HAD=30��
��HD=2��AH=2![]()
��CAH=45��
��CH=2![]()
��AC=2![]()
��AB=AC+CD=2![]() +2
+2![]() +2=10.2
+2=10.2![]() 10���ף���
10���ף���
����ô����۶�ǰ��Լ10�ף�