题目内容
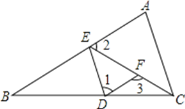
【题目】如图，在四边形
中，
的角平分线与边
交于点
，
的角平分线交直线
于点
.
（1）若点在四边形的内部，
①如图，若
，
，
，则
_______°；
②如图，试探索
、
、
之间的数量关系，并将你的探索过程写下来.
（2）如图，若点是四边形的外部，请你直接写出、、之间的数量关系.
【答案】（1）①
；②
；（2）
.
【解析】
（1）①根据平行线的性质和角平分线的定义可求∠BAE，∠CDO，再根据三角形外角的性质可求∠AEC，再根据四边形内角和等于360°可求∠DOE的度数；
②根据三角形外角的性质和角平分线的定义可得∠DOE和∠BAD、∠ADC的关系，再根据四边形内角和等于360°可求∠B、∠C、∠DOE之间的数量关系；
（2）根据四边形和三角形的内角和得到∠BAD+∠ADC=360°-∠B-∠C，∠EAD+∠ADO=180°-∠DOE，根据角平分线的定义得到∠BAD=2∠EAD，∠ADC=2∠ADO，于是得到结论．
解:（1）①）①∵AD∥BC，∠B=40°，∠C=70°，
∴∠BAD=140°，∠ADC=110°，
∵AE、DO分别平分∠BAD、∠CDA，
∴∠BAE=70°，∠ODC=55°，
∴∠AEC=110°，
∴∠DOE=360°-110°-70°-55°=125°；
故答案为：125；
②
平分
平分
.
（2）.
练习册系列答案
相关题目
【题目】为保护学生的身体健康，某中学课桌椅的高度都是按一定的关系配套设计的，下表列出5套符合条件的课桌椅的高度．
椅子高度x（cm） | 45 | 42 | 39 | 36 | 33 |
桌子高度y（cm） | 84 | 79 | 74 | 69 | 64 |
（1）假设课桌的高度为ycm，椅子的高度为xcm，请确定y与x的函数关系式；
（2）现有一把高38cm的椅子和一张高73.5cm的课桌，它们是否配套？为什么？
