题目内容
【题目】如图,在Rt△ABC中,∠C=90°,AB=10cm,AC=8cm.点P从点A出发沿AB方向向点B运动,速度为1cm/s,同时点Q从点B出发沿B→C→A方向向点A运动,速度为2cm/s.当一个动点到达终点时,另一个动点也随之停止运动.设运动时间为t(s).
(1)当t为何值时,△APC为等腰三角形.
(2)当点Q在线段BC上运动时,△PBQ的面积为S(cm2),写出S与t之间的函数关系.
(3)当点Q在线段BC上运动时,是否存在某一时刻t,使S△PBQ:S四边形APQC=5:3?若存在,求出t值;若不存在,说明理由.
(4)在运动过程中,是否存在某一时刻t,使BQ平分∠ABC?若存在,求出t的值;若不存在,请说明理由.
【答案】
(1)解:①当AP=PB时,∵∠ACB=90°,
∴CP=PA=PB,
∴t=5,
②当AC=AP时,t=8,
∴t=5s或8s时,△APC是等腰三角形
(2)解:当点Q在边BC上运动时,过点Q作QH⊥AB于H,
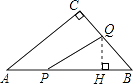
∵AP=xcm,
∴BP=(10﹣x)cm,BQ=2xcm,
∵△QHB∽△ACB,
∴ ![]() =
= ![]() ,
,
∴QH= ![]() xcm,
xcm,
y= ![]() BPQH=
BPQH= ![]() (10﹣x)
(10﹣x) ![]() x=﹣
x=﹣ ![]() x2+8x(0<x≤3)
x2+8x(0<x≤3)
(3)解:存在.∵S△PBQ:S四边形APQC=5:3,
∴﹣ ![]() x2+8x=
x2+8x= ![]() ×
× ![]() ×6×8,
×6×8,
解得x= ![]() 或
或 ![]() ,
,
∴t= ![]() s或
s或 ![]() s时,S△PBQ:S四边形APQC=5:3
s时,S△PBQ:S四边形APQC=5:3
(4)解:存在.如图作QH⊥AB于H.
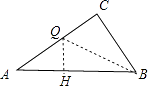
∵∠QBC=∠QBA,QC⊥BC,QH⊥AB,
∴QC=QH=2t﹣6,AQ=14﹣2t,
∵∠A=∠A,∠AHQ=∠C=90°,
∴△AQH∽△ABC,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴t= ![]() ,
,
∴t= ![]() s时,BQ平分∠ABC
s时,BQ平分∠ABC
【解析】(1)分两种情形讨论求解①当AP=PB时,可以证明CP=PA=PB,t=5,.②当AC=AP时;t=5,t=5s或8s时,△APC是等腰三角形
(2)当点Q在边BC上运动时,过点Q作QH⊥AB于H,由△QHB∽△ACB,推出 QHAC=QBAB 可得QH的长度, 根据y= 12 BPQH,列出式子即可;
(3)存在.由S△PBQ:S四边形APQC=5:3,可得关于x的方程,解方程即可解决问题;
(4)存在.如图作QH⊥AB于H.首先得出QC=QH=2t-6,AQ=14﹣2t,由△ AQH∽△ABC,可得 AQAB=QHBC ,从而列出方程, 解方程即可解决问题;
【考点精析】关于本题考查的三角形的面积和相似三角形的判定与性质,需要了解三角形的面积=1/2×底×高;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方才能得出正确答案.

 名校课堂系列答案
名校课堂系列答案【题目】列方程组解应用题:
为了保护环境,深圳某公交公司决定购买一批共10台全新的混合动力公交车,现有A、B两种型号,其中每台的价格,年省油量如下表:
A | B | |
价格(万元/台) | a | b |
节省的油量(万升/年) | 2.4 | 2 |
经调查,购买一台A型车比购买一台B型车多20万元,购买2台A型车比购买3台B型车少60万元.
(1)请求出a和b;
(2)若购买这批混合动力公交车每年能节省22.4万汽油,求购买这批混合动力公交车需要多少万元?





