题目内容
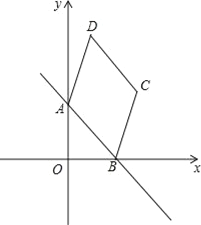
【题目】如图，在平面直角坐标系xOy中，直线
交y轴于点A，交x轴于点B，以线段AB为边作菱形ABCD（点C、D在第一象限），且点D的纵坐标为9．
（1）求点A、点B的坐标；
（2）求直线DC的解析式；
（3）除点C外，在平面直角坐标系xOy中是否还存在点P，使点A、B、D、P组成的四边形是平行四边形？若存在，请直接写出点P的坐标；若不存在，请说明理由．
【答案】（1）点A（0，4）；点B（
，0）．（2）直线DC的解析式为
．（3）点P的坐标为（
，﹣5）或（﹣
，13）．
【解析】（1）分别令一次函数中x=0、y=0，求出与之对应的y、x的值，由此即可得出点A、B的坐标；
（2）过点D作DE⊥y轴，垂足为E，由点D的纵坐标为9即可得出AE的长，根据菱形的性质得出AB=AD，结合勾股定理即可求出点D的坐标，由DC∥AB可设直线DC的解析式为
，代入点D的坐标求出b值即可得出结论；
（3）假设存在，点C时以BD为对角线找出的点，再分别以AB、AD为对角线，根据平行四边形的性质（对角线互相平分）结合点A、B、D的坐标即可得出点P的坐标．
解：（1）令
中x=0，则y=4，
∴点A（0，4）；
令
中y=0，则﹣
x+4=0，解得：x=2
，
∴点B（2
，0）．
（2）过点D作DE⊥y轴，垂足为E，如图1所示．
∵点D的纵坐标为9，OA=4，
∴AE=5．
∵四边形是ABCD是菱形，
∴AD=AB=
，
∴DE=
=
，
∴D（
，9）．
∵四边形是ABCD是菱形，
∴DC∥AB，
∴设直线DC的解析式为
，
∵直线DC过点D（
，9），
∴b=11，
∴直线DC的解析式为
．
（3）假设存在．
以点A、B、D、P组成的四边形是平行四边形还有两种情况（如图2）：
①以AB为对角线时，
∵A（0，4），B（2
，0），D（
，9），
∴点P（0+2
﹣
，4+0﹣9），即（
，﹣5）；
②以AD为对角线时，
∵A（0，4），B（2
，0），D（
，9），
∴点P（0+
﹣2
，4+9﹣0），即（﹣
，13）．
故除点C外，在平面直角坐标系xOy中还存在点P，使点A、B、D、P组成的四边形是平行四边形，点P的坐标为（
，﹣5）或（﹣
，13）．
“点睛”本题考查了一次函数图象上点的坐标特征、菱形的性质、勾股定理以及待定系数法求函数解析，解题的关键是：（1）分别代入x=0，y=0，求出与之对应的y、x的值；（2）求出点D的坐标；（3）分别以AB、AD为对角线求出点P的坐标.本题属于中档题，难度不大，解决该题型题目时，根据平行四边形的性质（对角线互相平分），结合三个顶点的坐标求出另一顶点坐标是关键.
