题目内容
某地区一种商品的需求量 (万件)、供应量
(万件)、供应量 (万件)与价格
(万件)与价格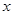 (元/件)分别近似满足下列函数关系式:
(元/件)分别近似满足下列函数关系式: ,
, .需求量为
.需求量为 时,即停止供应.当
时,即停止供应.当 时,该商品的价格称为稳定价格,需求量称为稳定需求量.
时,该商品的价格称为稳定价格,需求量称为稳定需求量.

(1)求该商品的稳定价格与稳定需求量;
(2)价格在什么范围,该商品的需求量低于供应量?
(3)当需求量高于供应量时,政府常通过对供应方提供价格补贴来提高供货价格,以提高供应量.现若要使稳定需求量增加4万件,政府应对每件商品提供多少元补贴,才能使供应量等于需求量?
 (万件)、供应量
(万件)、供应量 (万件)与价格
(万件)与价格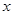 (元/件)分别近似满足下列函数关系式:
(元/件)分别近似满足下列函数关系式: ,
, .需求量为
.需求量为 时,即停止供应.当
时,即停止供应.当 时,该商品的价格称为稳定价格,需求量称为稳定需求量.
时,该商品的价格称为稳定价格,需求量称为稳定需求量.
(1)求该商品的稳定价格与稳定需求量;
(2)价格在什么范围,该商品的需求量低于供应量?
(3)当需求量高于供应量时,政府常通过对供应方提供价格补贴来提高供货价格,以提高供应量.现若要使稳定需求量增加4万件,政府应对每件商品提供多少元补贴,才能使供应量等于需求量?
(1)该商品的稳定价格为32元/件,稳定需求量为28万件(2)当价格大于32元/件而小于60元/件时,该商品的需求量代于供应量(3)6元
解:(1)当 时,有
时,有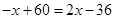 .··········· 2分
.··········· 2分
解这个方程,得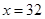 .此时
.此时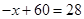 .
.
所以,该商品的稳定价格为32元/件,稳定需求量为28万件.········ 4分
(2)因为“需求量为 时,即停止供应”,所以,当
时,即停止供应”,所以,当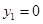 时,有
时,有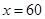 .
.
···································· 5分
又由图象,知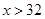 .·························· 7分
.·························· 7分
所以,当价格大于32元/件而小于60元/件时,该商品的需求量代于供应量.
···································· 8分
(3)设政府部门对该商品每件应提供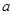 元补贴.根据题意,得方程组
元补贴.根据题意,得方程组
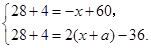 解这个方程组,得
解这个方程组,得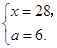 ············ 11分
············ 11分
所以,政府部门对该商品每件应提供6元的补贴. 12分
(1)根据 列出关于
列出关于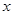 的方程即可
的方程即可
(2)法一:商品的需求量低于供应量也就是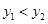 ,列出不等式即可,
,列出不等式即可,
法二:利用图象法,直线 在直线
在直线 的上方及
的上方及 时
时 范围
范围
(3)根据需求量和供应量都等于32(28+4)万件,列出方程组即可
 时,有
时,有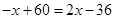 .··········· 2分
.··········· 2分解这个方程,得
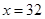 .此时
.此时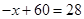 .
.所以,该商品的稳定价格为32元/件,稳定需求量为28万件.········ 4分
(2)因为“需求量为
 时,即停止供应”,所以,当
时,即停止供应”,所以,当 时,有
时,有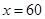 .
.···································· 5分
又由图象,知
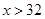 .·························· 7分
.·························· 7分所以,当价格大于32元/件而小于60元/件时,该商品的需求量代于供应量.
···································· 8分
(3)设政府部门对该商品每件应提供
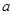 元补贴.根据题意,得方程组
元补贴.根据题意,得方程组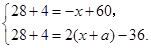 解这个方程组,得
解这个方程组,得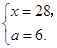 ············ 11分
············ 11分所以,政府部门对该商品每件应提供6元的补贴. 12分
(1)根据
 列出关于
列出关于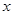 的方程即可
的方程即可(2)法一:商品的需求量低于供应量也就是
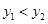 ,列出不等式即可,
,列出不等式即可,法二:利用图象法,直线
 在直线
在直线 的上方及
的上方及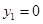 时
时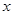 范围
范围(3)根据需求量和供应量都等于32(28+4)万件,列出方程组即可

练习册系列答案
相关题目
 的面积为
的面积为 ,点P的运动时间为t秒,求S与t之间的函数关系式(要求写出自变量t的取值范围);
,点P的运动时间为t秒,求S与t之间的函数关系式(要求写出自变量t的取值范围);

 所在直线的解析式.
所在直线的解析式. 地逆流而上,前往
地逆流而上,前往 地营救受困群众,途经
地营救受困群众,途经 地时,由所携带的救生艇将
地时,由所携带的救生艇将 (千米)和冲锋舟出发后所用时间
(千米)和冲锋舟出发后所用时间 (分)之间的函数图象如图所示.假设营救群众的时间忽略不计,水流速度和冲锋舟在静水中的速度不变.
(分)之间的函数图象如图所示.假设营救群众的时间忽略不计,水流速度和冲锋舟在静水中的速度不变.
 ,假设群众上下船的时间不计,求冲锋舟在距离
,假设群众上下船的时间不计,求冲锋舟在距离

 (千克)与月份
(千克)与月份
 的关系如下表所示:
的关系如下表所示: (千克)与月份
(千克)与月份 的函数关系为:
的函数关系为: ;
; (元)与月份
(元)与月份 的函数关系为:
的函数关系为: ;而在6到12月每千克桃脯的价格
;而在6到12月每千克桃脯的价格 (元)与月份
(元)与月份
 ,且其中的
,且其中的 是用于出口,剩余部分由经销点国内销售,每月出口桃脯的售价每千克降低了
是用于出口,剩余部分由经销点国内销售,每月出口桃脯的售价每千克降低了 ,而国内销售的桃脯价格每千克上涨了
,而国内销售的桃脯价格每千克上涨了 ,这样该经销点1到4月销售桃脯的总额为142560元,试求出
,这样该经销点1到4月销售桃脯的总额为142560元,试求出 的值.
的值.  ,
,  ,
,  ,
,  )
) 与y轴的交点坐标是( ).
与y轴的交点坐标是( ). )
)  )
)