题目内容
【题目】如图①,已知抛物线![]() 的顶点为点P,与y轴交于点B.点A坐标为(3,2).点M为抛物线上一动点,以点M为圆心,MA为半径的圆交x轴于C,D两点(点C在点D的左侧).
的顶点为点P,与y轴交于点B.点A坐标为(3,2).点M为抛物线上一动点,以点M为圆心,MA为半径的圆交x轴于C,D两点(点C在点D的左侧).

(1)如图②,当点M与点B重合时,求CD的长;
(2)当点M在抛物线上运动时,CD的长度是否发生变化?若变化,求出CD关于点M横坐标x的函数关系式;若不发生变化,求出CD的长;
(3)当△ACP与△ADP相似时,求出点C的坐标.
【答案】(1) CD=4;(2)不发生变化,CD=4;(3)点C坐标为:(1,0),![]() ,
,![]()
【解析】
(1)如图,先利用勾股定理求MC的长和OC的长,再利用垂径定理求得CD的长度;
(2)如图所示,过点M作MH⊥x轴,垂足为H,连接AM、MC,由勾股定理可知![]() ,CH=2,结合垂径定理可求得CD的长;
,CH=2,结合垂径定理可求得CD的长;
(3)分为点M与点P重合,点M在点P的左侧,点M在点P的右侧三种情况画出图形,然后依据相似三角形的对应边成比例可求得OC的长,从而可求得点C的坐标;
(1)如图:连结BC,BD,
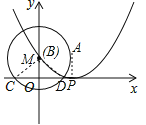
由题意得:![]() ,(3,2),
,(3,2),
∴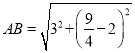 ,
,
∴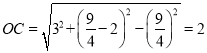 ,
,
∴CD=2OC=4;
(2)如图:作MH⊥x轴,连结MA,MC,
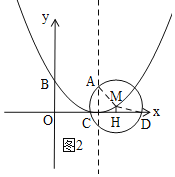
设![]() ,则半径
,则半径![]() ,
,
∴![]() =
=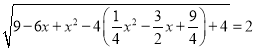 ,
,
∵MH⊥CD,
∴CD=2CH=4,
(3)①当△APC∽△APD,即全等时,
∴PC=PD,P与M重合,
∵P(3,0),CD=4,
∴C(1,0)
②如图,点M在点P的左侧,
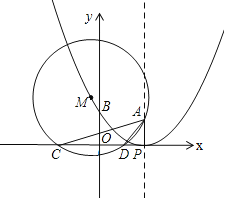
△APC∽△DPA,![]() ,
,
设PC=x,x(x-4)=4,解得![]() (舍去负值),
(舍去负值),
∴![]() ,
,
③如图,点M在点P的右侧
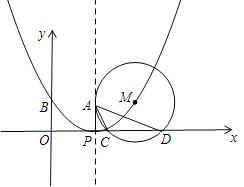
△APC∽△DPA,![]() ,
,
设PC=x,x(x+4)=4,解得![]() (舍去负值),
(舍去负值),
∴![]() ,
,
综上所述,点C坐标为:C(1,0);![]() ;
;![]() ;
;

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目