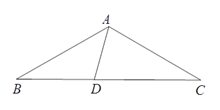题目内容
【题目】如图,在△ABC中,∠ACB=90°,AC=4,BC=3,D是边AC的中点,CE⊥BD交AB于点E.
(1)求tan∠ACE的值;
(2)求AE:EB.

【答案】(1)![]() (2)8:9
(2)8:9
【解析】试题分析:(1)根据同角的余角相等可证得: ∠ACE=∠CBD,因为点D是AC的中点,所以CD=2,所以tan∠ACE=tan∠CBD=![]() ,(2) 过A作AC的垂线交CE的延长线于P,
,(2) 过A作AC的垂线交CE的延长线于P,
在△CAP中,CA=4,∠CAP=90°,所以tan∠ACP=![]() ,所以AP=
,所以AP=![]() ,又因为∠ACB=90°,
,又因为∠ACB=90°,
∠CAP=90°,可证得BC∥AP, 所以AE:EB=AP:BC=8:9.
试题解析:(1)因为∠ACB=90°,CE⊥BD,
所以∠ACE=∠CBD,
在△BCD中,BC=3,CD=![]() AC=2,∠BCD=90°,
AC=2,∠BCD=90°,
tan∠CBD=![]() ,
,
即tan∠ACE=![]() .
.
(2)过A作AC的垂线交CE的延长线于P,
则在△CAP中,CA=4,∠CAP=90°,tan∠ACP=![]() ,
,
得AP=![]() ,
,
又∠ACB=90°,∠CAP=90°,得BC∥AP,
得AE:EB=AP:BC=8:9.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目