Question

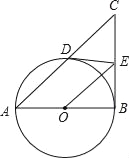
【题目】如图，在△ABC中，AD是高，CE是中线，DG垂直平分CE，连接DE．

（1）求证：DC＝BE；

（2）若∠AEC＝72°，求∠BCE的度数．

Answer 1

【答案】（1）证明见解析；（2）24°

【解析】

（1）根据线段垂直平分线的性质可得DE＝DC，根据直角三角形斜边上的中线等于斜边的一半可得DE＝BE，等量代换即可得证；

（2）根据等边对等角以及三角形外角的性质可得∠B＝∠EDB＝2∠BCE，然后根据∠AEC＝∠B+∠BCE＝72°可求∠BCE的度数.

(1)证明：∵DG垂直平分CE，

∴DE＝DC，

∵AD是高，CE是中线，

∴DE是Rt△ADB的斜边AB上的中线，

∴DE＝AB＝BE，

∴DC＝BE；

(2)∵DE＝DC，

∴∠DEC＝∠DCE，

∴∠EDB＝∠DEC＋∠BCE＝2∠BCE

∵DE＝BE

∴∠B＝∠EDB

∴∠B＝2∠BCE，

∴∠AEC＝3∠BCE＝72°，

∴∠BCE＝24°.