题目内容
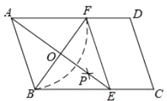
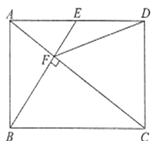
【题目】如图，在矩形
中，
是
边的中点，
，垂足为点
，连接
．则列四个结论：
①
；②
；③
；④
．其中正确的结论有：
A.4个B.3个C.2个D.1个
【答案】A
【解析】
①通过证明
及对顶角相等即可得到答案；
②根据
是
边的中点及①中的相似可得
可得答案；
③过D作DM∥BE交AC于N，利用平行四边形的性质证明DM垂直平分CF可得答案；
④由①中的相似得到
，设
，利用母子三角形的性质求出
可得答案．
解：①如图，∵四边形ABCD是矩形，∴AD∥BC，
，
又因为：
，
所以：
，故①成立，
②因为：E是的中点，所以：
，
因为：，
所以：
，
设
则
，
所以：
，所以
，故②成立，
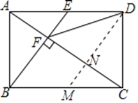
③过D作DM∥BE交AC于N，
∵DE∥BM，BE∥DM，
∴四边形BMDE是平行四边形，
∴BM=DE=
BC，∴BM=CM， ∴CN=NF，
∵BE⊥AC于点F，DM∥BE，
∴DN⊥CF，
∴DM垂直平分CF，
∴DF=DC，故③正确；
④因为：
，设
，则
，
所以：
，
，
因为：，所以：
，
所以：
，所以④成立；
故选A．
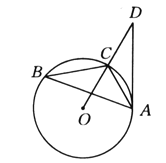
举一反三单元同步过关卷系列答案【题目】如图，平行四边形ABCD中，O是对角线BD的中点，过点O的直线EF分别交DA，BC的延长线于E，F．
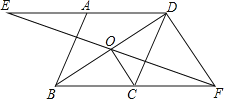
（1）求证：AE＝CF；
（2）若AE＝BC，试探究线段OC与线段DF之间的关系，并说明理由．
【题目】某市A，B两个蔬菜基地得知四川C，D两个灾民安置点分别急需蔬菜240t和260t的消息后，决定调运蔬菜支援灾区，已知A蔬菜基地有蔬菜200t，B蔬菜基地有蔬菜300t，现将这些蔬菜全部调运C，D两个灾区安置点.从A地运往C，D两处的费用分别为每吨20元和25元，从B地运往C，D两处的费用分别为每吨15元和18元.设从B地运往C处的蔬菜为x吨.
（1）请填写下表，并求两个蔬菜基地调运蔬菜的运费相等时x的值；
C | D | 总计/t | |
A | 200 | ||
B | x | 300 | |
总计/t | 240 | 260 | 500 |
（2）设A，B两个蔬菜基地的总运费为w元，求出w与x之间的函数关系式，并求
总运费最小的调运方案；
（3）经过抢修，从B地到C处的路况得到进一步改善，缩短了运输时间，运费每吨减少m元（m＞0），其余线路的运费不变，试讨论总运费最小的调动方案.
