题目内容
如图，已知△ABC中，AB=AC，AF是BC边上的中线，D是BA延长线上一点，点E在AC上，且AD=AE。
求证：DE⊥BC。
求证：DE⊥BC。
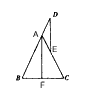
证明：因为AB=AC，BF=CF，
所以∠BAF=∠CAF，AF⊥BC，
因为AD=AE，
所以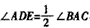
，
所以∠BAF=∠D，
所以DE//AF，
所以DE⊥BC。
练习册系列答案
相关题目
题目内容
证明：因为AB=AC，BF=CF，
所以∠BAF=∠CAF，AF⊥BC，
因为AD=AE，
所以，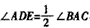
所以∠BAF=∠D，
所以DE//AF，
所以DE⊥BC。
如图，已知△ABC中，AB=AC，E、F分别在AB、AC上且AE=CF．
如图，已知△ABC中，P是AB上一点，连接CP，以下条件不能判定△ACP∽△ABC的是（ ）
（2012•梓潼县一模）如图，已知△ABC中，∠C=90°，AC=4，BC=3，则sinA=（ ）
如图，已知△ABC中，BC=8，BC边上的高h=4，D为BC上一点，EF∥BC交AB于E，交AC于F（EF不过A、B），设E到BC的距离为x，△DEF的面积为y，那么y关于x的函数图象大致是（ ）
如图，已知△ABC中，AB=AC，D是BC中点，则下列结论不正确的是（ ）