题目内容
某生物小组观察一植物生长,得到植物高度y(单位:厘米)与观察时间x(单位:天)的关系,并画出如图所示的图象(AC是线段,直线CD平行x轴).
(1)该植物从观察时起,多少天以后停止长高?
(2)求直线AC的解析式,并求该植物最高长多少厘米?
解:(1)∵CD∥x轴,
∴从第50天开始植物的高度不变。
答:该植物从观察时起,50天以后停止长高。
(2)设直线AC的解析式为y=kx+b(k≠0),
∵经过点A(0,6),B(30,12),
∴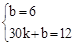 ,解得
,解得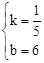 。
。
∴直线AC的解析式为y= x+6(0≤x≤50)。
x+6(0≤x≤50)。
当x=50时,y= ×50+6=16。
×50+6=16。
答:直线AC的解析式为y= x+6(0≤x≤50),该植物最高长16cm。
x+6(0≤x≤50),该植物最高长16cm。
解析试题分析:(1)根据平行线间的距离相等可知50天后植物的高度不变,也就是停止长高。
(2)设直线AC的解析式为y=kx+b(k≠0),然后利用待定系数法求出直线AC的解析式,再把x=50代入进行计算即可得解。

练习册系列答案
相关题目
某商场计划购进A,B两种新型节能台灯共100盏,这两种台灯的进价、售价如表所示:
| 类型 价格 | 进价(元/盏) | 售价(元/盏) |
| A型 | 30 | 45 |
| B型 | 50 | 70 |
(2)若商场规定B型台灯的进货数量不超过A型台灯数量的3倍,应怎样进货才能使商场在销售完这批台灯时获利最多?此时利润为多少元?
 ,﹣
,﹣ 的图象与x轴交于两个不同的点A(﹣2,0)、B(4,0),与y轴交于点C(0,3),连接BC、AC,该二次函数图象的对称轴与x轴相交于点D.
的图象与x轴交于两个不同的点A(﹣2,0)、B(4,0),与y轴交于点C(0,3),连接BC、AC,该二次函数图象的对称轴与x轴相交于点D.

 的图象与一次函数
的图象与一次函数 的图象交于点A(1,4)和点B
的图象交于点A(1,4)和点B ,
, ).
).
 >0时,直接写出
>0时,直接写出 >
>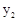 时自变量
时自变量 的图象交于A(2,4)、B(﹣4,n)两点.
的图象交于A(2,4)、B(﹣4,n)两点.
