题目内容
已知:二次函数y=x2-2(m-1)x-1-m的图象与x轴交于点A(x1,0)、点B(x2,0)(x1<0<x2),与y轴交于点C
(1)求m的取值范围;
(2)若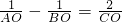 ,求这个二次函数的解析式.
,求这个二次函数的解析式.
解:(1)∵x1<0<x2,
∴x1x2=-m-1<0,
∴m>-1.
(2)∵x1<0<x2,
∴AO=-x1,OB=x2,
∵m>-1,
∴CO=|-m-1|=m+1,
∵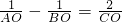 ,
,
∴CO(OB-OA)=2AO•OB,
即(m+1)(x1+x2)=-2x1x2,
∴(m+1)•2(m-1)=2(m+1),
∴m=-1(舍去)或m=2.
∴二次函数的解析式为y=x2-2x-3.
分析:(1)根据x1<0<x2可以得到x1x2=-m-1<0,并由此求得m的取值范围;
(2)根据x1<0<x2表示出AO=-x1,OB=x2,CO=|-m-1|=m+1,再根据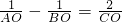 ,得到CO(OB-OA)=2AO•OB,并由此得到有关m的方程(m+1)•2(m-1)=2(m+1),解得m值后即可求得二次函数的解析式.
,得到CO(OB-OA)=2AO•OB,并由此得到有关m的方程(m+1)•2(m-1)=2(m+1),解得m值后即可求得二次函数的解析式.
点评:本题考查了二次函数的综合知识,解题时要综合利用一元二次方程根与系数的关系和已知条件得到待定系数的方程,从而求解.
∴x1x2=-m-1<0,
∴m>-1.
(2)∵x1<0<x2,
∴AO=-x1,OB=x2,
∵m>-1,
∴CO=|-m-1|=m+1,
∵
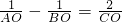 ,
,∴CO(OB-OA)=2AO•OB,
即(m+1)(x1+x2)=-2x1x2,
∴(m+1)•2(m-1)=2(m+1),
∴m=-1(舍去)或m=2.
∴二次函数的解析式为y=x2-2x-3.
分析:(1)根据x1<0<x2可以得到x1x2=-m-1<0,并由此求得m的取值范围;
(2)根据x1<0<x2表示出AO=-x1,OB=x2,CO=|-m-1|=m+1,再根据
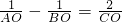 ,得到CO(OB-OA)=2AO•OB,并由此得到有关m的方程(m+1)•2(m-1)=2(m+1),解得m值后即可求得二次函数的解析式.
,得到CO(OB-OA)=2AO•OB,并由此得到有关m的方程(m+1)•2(m-1)=2(m+1),解得m值后即可求得二次函数的解析式.点评:本题考查了二次函数的综合知识,解题时要综合利用一元二次方程根与系数的关系和已知条件得到待定系数的方程,从而求解.

练习册系列答案
相关题目
 已知:二次函数的表达式为y=2x2+4x-1.
已知:二次函数的表达式为y=2x2+4x-1.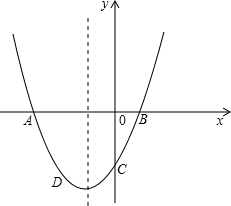 交于点C,点D(-2,-3)在抛物线上.
交于点C,点D(-2,-3)在抛物线上.