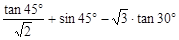题目内容
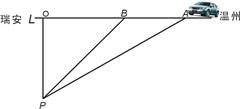
某市在城市建设中要拆除旧烟囱AB(如图所示),在烟囱正西方向的楼CD的顶端C处测得烟囱的顶端A的仰角为45°,底端B的俯角为30°,已量得DB=21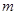 .
.
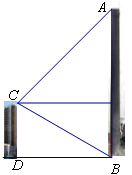
(1)在原图上画出点C望点A的仰角和点C望点B的俯角,并分别标出仰角和俯角的大小;
(2)拆除时若让烟囱向正东倒下,试问:距离烟囱东方35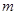 远的一棵大树是否被歪倒的烟囱砸着?请说明理由.
远的一棵大树是否被歪倒的烟囱砸着?请说明理由.
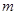 .
.
(1)在原图上画出点C望点A的仰角和点C望点B的俯角,并分别标出仰角和俯角的大小;
(2)拆除时若让烟囱向正东倒下,试问:距离烟囱东方35
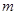 远的一棵大树是否被歪倒的烟囱砸着?请说明理由.
远的一棵大树是否被歪倒的烟囱砸着?请说明理由. (1)如图所示:
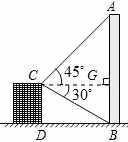
(2)这棵大树不会被歪倒的烟囱砸着.

(2)这棵大树不会被歪倒的烟囱砸着.
试题分析:(1)向上的视线与水平线的夹角为仰角;向下的视线与水平线的夹角为俯角.
(2)过点C作CG⊥AB于点G.把求AB的问题转化求AG与BG的长,从而可以在△ACG和△BCG中利用三角函数求解.
(1)如图所示:

(2)这棵大树不会被歪倒的烟囱砸着.
∵在RT△AGC中,∠ACG=45°.
∴AG=CG=DB=21(m).
在Rt△BCG中,BG=CG×tan30°=DB×tan30°=21×

∴烟囱的高度
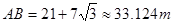
∵33.124m<35m.
∴这棵大树不会被歪倒的烟囱砸着.
点评:解决一般三角形的问题,可以转化为直角三角形的问题,转化的方法是作高线.

练习册系列答案
相关题目
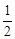
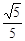
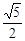
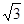 海里问此时是否需要向此未经特许的船只发出警告,命令其不得进入我国领海?
海里问此时是否需要向此未经特许的船只发出警告,命令其不得进入我国领海?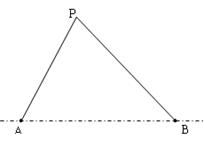
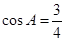 ,则下列结论正确的为 ( )
,则下列结论正确的为 ( )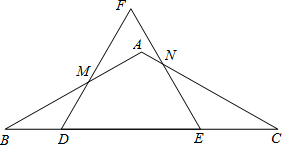
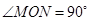 ,矩形ABCD的顶点A、B分别在边OM 、ON上运动,且形状和大小保持不变,其中AB=4,BC=3.
,矩形ABCD的顶点A、B分别在边OM 、ON上运动,且形状和大小保持不变,其中AB=4,BC=3.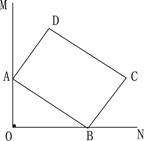
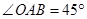 时,OA的长为 ;
时,OA的长为 ;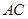 ∥
∥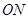 时,求OA的长;
时,求OA的长;