题目内容
【题目】在等腰△ABC与等腰△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,且点D、E、C三点在同一条直线上,连接BD.
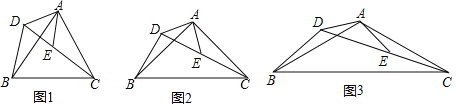
(1)如图1,求证:△ADB≌△AEC
(2)如图2,当∠BAC=∠DAE=90°时,试猜想线段AD,BD,CD之间的数量关系,并写出证明过程;
(3)如图3,当∠BAC=∠DAE=120°时,请直接写出线段AD,BD,CD之间的数量关系式为: (不写证明过程)
【答案】(1)见解析;(2)CD=![]() AD+BD,理由见解析;(3)CD=
AD+BD,理由见解析;(3)CD=![]() AD+BD
AD+BD
【解析】
(1)由“SAS”可证△ADB≌△AEC;
(2)由“SAS”可证△ADB≌△AEC,可得BD=CE,由直角三角形的性质可得DE=![]() AD,可得结论;
AD,可得结论;
(3)由△DAB≌△EAC,可知BD=CE,由勾股定理可求DH=![]() AD,由AD=AE,AH⊥DE,推出DH=HE,由CD=DE+EC=2DH+BD=
AD,由AD=AE,AH⊥DE,推出DH=HE,由CD=DE+EC=2DH+BD=![]() AD+BD,即可解决问题;
AD+BD,即可解决问题;
证明:(1)∵∠BAC=∠DAE,
∴∠BAD=∠CAE,
又∵AB=AC,AD=AE,
∴△ADB≌△AEC(SAS);
(2)CD=![]() AD+BD,
AD+BD,
理由如下:∵∠BAC=∠DAE,
∴∠BAD=∠CAE,
又∵AB=AC,AD=AE,
∴△ADB≌△AEC(SAS);
∴BD=CE,
∵∠BAC=90°,AD=AE,
∴DE=![]() AD,
AD,
∵CD=DE+CE,
∴CD=![]() AD+BD;
AD+BD;
(3)作AH⊥CD于H.
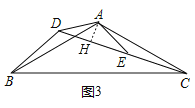
∵∠BAC=∠DAE,
∴∠BAD=∠CAE,
又∵AB=AC,AD=AE,
∴△ADB≌△AEC(SAS);
∴BD=CE,
∵∠DAE=120°,AD=AE,
∴∠ADH=30°,
∴AH=![]() AD,
AD,
∴DH=![]() =
=![]() AD,
AD,
∵AD=AE,AH⊥DE,
∴DH=HE,
∴CD=DE+EC=2DH+BD=![]() AD+BD,
AD+BD,
故答案为:CD=![]() AD+BD.
AD+BD.