题目内容
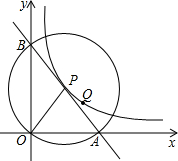 (2012•峨边县模拟)如图,在平面直角坐标系中,O为坐标原点,P是反比例函数y=
(2012•峨边县模拟)如图,在平面直角坐标系中,O为坐标原点,P是反比例函数y=| 6 | x |
(1)判断P是否在线段AB上,并说明理由;
(2)求△AOB的面积.
分析:(1)由P在⊙O上,而∠AOB=90°,根据圆周角定义的推论得AB是⊙P的直径,即可得到点P在线段AB上;
(2)过点P作PP1⊥x轴,PP2⊥y轴,设P(a,b),由P点为圆心可得PP1、PP2是△AOB的中位线,则S△AOB=
OA×OB=
×2PP1×2PP2=2ab,再根据P点在反比例函数y=
(x>0)图象上的点得到ab=6,把ab=6代入即可得到△AOB的面积.
(2)过点P作PP1⊥x轴,PP2⊥y轴,设P(a,b),由P点为圆心可得PP1、PP2是△AOB的中位线,则S△AOB=
| 1 |
| 2 |
| 1 |
| 2 |
| 6 |
| x |
解答:解:(1)点P在线段AB上.理由如下:
∵PO为半径,
∴点O在⊙P上,
而∠AOB=90°,
∴AB是⊙P的直径,
∴点P在线段AB上;
 (2)过点P作PP1⊥x轴,PP2⊥y轴,设P(a,b),如图,
(2)过点P作PP1⊥x轴,PP2⊥y轴,设P(a,b),如图,
由题意可知PP1、PP2是△AOB的中位线,
∴S△AOB=
OA×OB=
×2PP1×2PP2=2ab,
∵P是反比例函数y=
(x>0)图象上的任意一点,
∴ab=6,
∴S△AOB=2×6=12.
∵PO为半径,
∴点O在⊙P上,
而∠AOB=90°,
∴AB是⊙P的直径,
∴点P在线段AB上;
 (2)过点P作PP1⊥x轴,PP2⊥y轴,设P(a,b),如图,
(2)过点P作PP1⊥x轴,PP2⊥y轴,设P(a,b),如图,由题意可知PP1、PP2是△AOB的中位线,
∴S△AOB=
| 1 |
| 2 |
| 1 |
| 2 |
∵P是反比例函数y=
| 6 |
| x |
∴ab=6,
∴S△AOB=2×6=12.
点评:本题考查了反比例函数y=
(k≠0)图象上点的坐标特点:所有点的横纵坐标之积等于k.也考查了圆周角定理的推论以及三角形的面积公式.
| k |
| x |

练习册系列答案
相关题目

 (2012•峨边县模拟)如图,A(1,-3),B(4,-1),P(a,0),N(a+2,0),当四边形ABNP的周长最小时,a=
(2012•峨边县模拟)如图,A(1,-3),B(4,-1),P(a,0),N(a+2,0),当四边形ABNP的周长最小时,a= (2012•峨边县模拟)如图,AD∥BC,∠A=90°,BC=BD,CE⊥BD.
(2012•峨边县模拟)如图,AD∥BC,∠A=90°,BC=BD,CE⊥BD.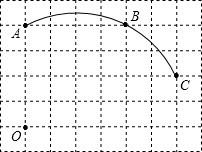 (2012•峨边县模拟)如图在单位长度为1的正方形网格中,一段圆弧经过网格的交点A、B、C.
(2012•峨边县模拟)如图在单位长度为1的正方形网格中,一段圆弧经过网格的交点A、B、C.