题目内容
已知函数y=(2m–2)x+m+1 (1)、m为何值时,图象过原点.(2)、已知y随x增大而增大,求m的取值范围.(3)、函数图象与y轴交点在x轴上方,求m取值范围.(4)、图象过二、一、四象限,求m的取值范围.
(1)、m=-1 (2)、m>1 (3)、m>-1 (4)、-1<m<1
分析:
(1)把原点坐标代入函数解析式即可求得m的值;
(2)y随x增大而增大,说明2m-2>0,图象与y轴交点在x轴上方;
(3)函数图象与y轴交点在x轴上方,说明m+1>0,求解不等式组即可;
(4)图象过二、一、四象限,说明2m-2<0且m+1>0, 求解不等式组即可.
解答:
(1)把(0,0)代入y=(2m-2)x+m+1,得
(2m-2)×0+m+1=0,解得:m=-1。
(2)根据题意:2m-2>0,解得:m>1。
(3)根据题意:m+1>0, 解得:m>-1。
(4)根据题意:2m-2<0,解得:m<1;又m+1>0, 解得:m>-1,所以m的取值范围为-1<m<1。
点评:本题考查图象经过点的含义和一次函数的性质,图象经过点,则点的坐标满足函数关系式;k>0,y随x的增大而增大,k<0,y随x的增大而减小。

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
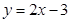 的图像与x轴交点坐标为________,与y轴的交点坐标为____________。
的图像与x轴交点坐标为________,与y轴的交点坐标为____________。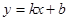 经过点(1,2)和点(
经过点(1,2)和点(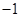 ,4),求这条直线的解析式.
,4),求这条直线的解析式.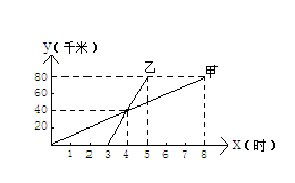
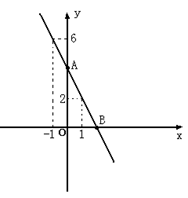
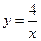 的图像交于 A(2,2),B(-1,m),求一次函数的解析式.
的图像交于 A(2,2),B(-1,m),求一次函数的解析式. 拟台球游戏,为简单起见,约定:①每个球袋视为一个点,如果不遇到障碍,各球均沿直线前进;②A球击B球,意味着B球在A球前进的路线上,且B球被撞击后沿A球原来的方向前进;③球撞击桌边后的反弹角度等于入射角度,(如图中∠β=∠a)如图所示,设桌边只剩下白球,A,6号球B。
拟台球游戏,为简单起见,约定:①每个球袋视为一个点,如果不遇到障碍,各球均沿直线前进;②A球击B球,意味着B球在A球前进的路线上,且B球被撞击后沿A球原来的方向前进;③球撞击桌边后的反弹角度等于入射角度,(如图中∠β=∠a)如图所示,设桌边只剩下白球,A,6号球B。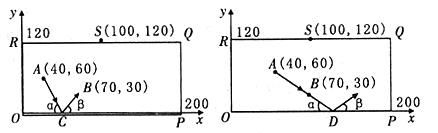

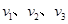 且
且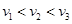 ,则小可骑车上学时,离家的距离s与所用时间t的函数关系图像大致是
,则小可骑车上学时,离家的距离s与所用时间t的函数关系图像大致是