题目内容
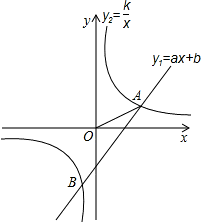 如图,点A(3,1),B(-1,n)是一次函数y1=ax+b 和反比例函数y2=
如图,点A(3,1),B(-1,n)是一次函数y1=ax+b 和反比例函数y2= 图象的交点,
图象的交点,
(1)求两个函数的解析式
(2)观察图象直接写出y1≥y2自变量x的取值范围.
(3)在平面内求一点M,使△AOM是以OA为直角边等腰直角三角形.
如果还存在其他点M,直接写出答案.
 (1)解:把A(3,1)代入y2=
(1)解:把A(3,1)代入y2= 得:k=xy=3,
得:k=xy=3,∴y2=
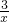 ,
,把x=-1代入上式得:y=-3,
∴B(-1,-3),
把A、B的坐标代入y1=ax+b得:
 ,
,解得:a=1,b=-2,
∴y1=x-2,
即一次函数的解析式是y1=x-2,反比例函数的解析式是y2=
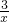 .
.(2)解:根据图象可知:y1≥y2自变量x的取值范围-1≤x<0或x≥3.
(3)解:符合条件的点M的坐标是(1,-3),(4,-2),(-1,3),(2,4),
选(1,-3),
证明:如图作AN⊥y轴,MD⊥y轴,垂足分别为N,D.
∵△AOM是等腰三角形且OA是直角边,
∴OA=OM,∠AOM=90°,
∵∠NOA+∠AOM+∠MOD=180°,
∴∠NOA+∠MOD=90°,
∵MD⊥y轴,
∴∠ODM=90°,
∴∠MOD+∠OMD=180°-90°=90°,
∵∠NOA+∠MOD=90°,
∠MOD+∠OMD=90°,
∴∠NOA=∠OMD,
∵AN⊥y轴,MD⊥y轴,
∴∠ANO=∠MDO=90°,
在△AON和△NMD中,
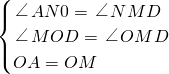 ,
,∴△AON≌△NMD (AAS),
∴AN=OD,ON=DM,
∵A(1,3),
∴AN=3,ON=1,
∴OD=3,DM=1,
∴M(1,-3).
分析:(1)把A的坐标代入反比例函数的解析式,求出k,把B的坐标代入反比例函数的解析式,能求出B的坐标,把A、B的坐标代入一次函数的解析式得出关于a、b的方程组,求出方程组的解即可;
(2)根据图象和一次函数与反比例函数的交点坐标,即可得出答案
(3)选M(1,-3),作AN⊥y轴,MD⊥y轴,垂足分别为N,D.证出∠NAO=MOD,根据AAS证△NAO≌△DOM证出AN=OD,MD=ON,根据A的坐标求出即可.
点评:本题考查了一用待定系数法求一次函数、反比例函数的解析式,全等三角形的性质和判定,一次函数与反比例函数的交点问题等知识点的运用,此题综合性比较强,主要培养了学生综合运用性质进行推理和计算的能力,同时也培养了学生的观察图形的能力,用了数形结合思想.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
 如图,点A的坐标为(2
如图,点A的坐标为(2| 2 |
| A、(0,0) | ||||||||
B、(
| ||||||||
| C、(1,1) | ||||||||
D、(
|
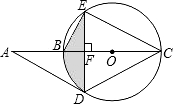 BE、CD、CE,已知∠BED=30°.
BE、CD、CE,已知∠BED=30°.
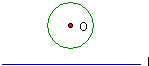 12、如图,点O到直线l的距离为3,如果以点O为圆心的圆上只有两点到直线l的距离为1,则该圆的半径r的取值范围是
12、如图,点O到直线l的距离为3,如果以点O为圆心的圆上只有两点到直线l的距离为1,则该圆的半径r的取值范围是