题目内容
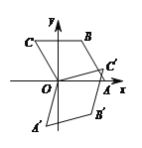
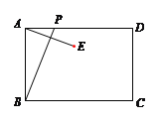
【题目】如图,已知矩形ABCD中,AB=4,动点P从点A出发,沿AD方向以每秒1个单位的速度运动,连接BP,作点A关于直线BP的对称点E,设点P的运动时间为t(s).在动点P在射线AD上运动的过程中,则使点E到直线BC的距离等于3时对应的t的值为______.
【答案】![]() 或
或![]()
【解析】
分两种情况:①当点E在BC的上方,点E到BC的距离为3,作EM⊥BC于M,延长ME交AD于N,连接PE、BE,则EM=3,EN=1,BE=AB=4,四边形ABMN是矩形,AN=BM=![]() ,得出△BME∽△ENP,得出
,得出△BME∽△ENP,得出![]() ,求出NP=
,求出NP=![]() ,即可得出结果;
,即可得出结果;
②当点E在BC的下方,点E到BC的距离为3,作EH⊥AB的延长线于H,则BH=3,BE=AB=4,AH=AB+BH=7,HE=![]() ,得△AHE∽△PAB,得出
,得△AHE∽△PAB,得出![]() ,即可得出结果.
,即可得出结果.
①当点E在BC的上方,点E到BC的距离为3,作EM⊥BC于M,延长ME交AD于N,连接PE、BE,如图1所示:

则EM=3,EN=1,BE=AB=4,四边形ABMN是矩形,
在Rt△EBM中,AN=BM=![]() ,
,
∵点A、E关于直线BP对称,
∴∠PEB=∠PAB=90°,
∵∠ENP=∠EMB=∠PEB=90°,
∴∠PEN=∠EBM,
∴△BME∽△ENP,
∴![]() ,即
,即![]() ,
,
∴NP=![]() ,
,
∴t=AP=AN-NP=;
②当点E在BC的下方,点E到BC的距离为3,作EH⊥AB的延长线于H,如图2所示:
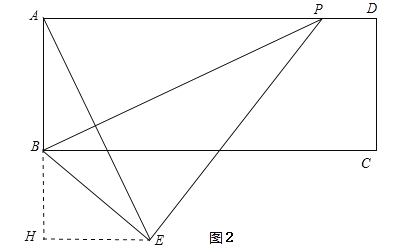
则BH=3,BE=AB=4,AH=AB+BH=7,
在Rt△BHE中,HE=![]() ,
,
∵∠PAB=∠BHE=90°,AE⊥BP,
∴∠APB+∠EAP=∠HAE+∠EAP=90°,
∴∠HAE=∠APB,
∴△AHE∽△PAB,
∴![]() ,即
,即![]() ,
,
解得:t=AP=4![]() ,
,
综上所述,t=![]() 或4
或4![]() .
.

练习册系列答案
相关题目