题目内容
【题目】己知,![]() 满足
满足![]() 点在
点在![]() 轴的负半轴上,直角顶点
轴的负半轴上,直角顶点![]() 在
在![]() 轴上,点
轴上,点![]() 在
在![]() 轴上方.
轴上方.
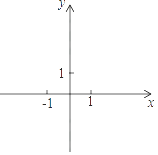
![]() 如图1所示,若点
如图1所示,若点![]() 与原点重合,点
与原点重合,点![]() 的坐标是
的坐标是![]() ,则点
,则点![]() 的坐标是 ;
的坐标是 ;

![]() 如图2所示,若点
如图2所示,若点![]() 的坐标是
的坐标是![]() ,过点
,过点![]() 作
作![]() 轴于
轴于![]() ,请求出点
,请求出点![]() 的坐标.
的坐标.

【答案】(1)(﹣2,0);(2)(-3,0)
【解析】
(1)根据点C(0,2)、BC=BA可得点A坐标;
(2)证明△ABO≌△BCD,得到BO=CD,OA=DB=OD+OB=OD+CD,即可解答;
(1)∵点C(0,2),O与B重合,∴BC=BA=2,∴点A的坐标为(﹣2,0);
(2)∵点C的坐标是(1,2),
∴CD=1,OD=2,
∵CD⊥y轴,
∴∠CDB=90°,∠DCB+∠CBD=90°,
∵∠ABC=90°,
∴∠ABO+∠CBD=90°,
∴∠ABO=∠DCB,
在△ABO和△BCD中,
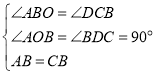
∴△ABO≌△BCD,
∴BO=CD=1,OA=DB,
∴BD=OB+OD=3,
∴OA=3,点A的坐标为(-3,0).

【题目】10月21日,“中国流动科技馆”巡展启动仪式在新华区青少年活动中心盛大举行,此次巡展以“体验科学”为主题.该区某中学举行了“科普知识”竞赛,为了解此次“科普知识”竞赛成绩的情况,随机抽取了部分参赛学生的成绩,整理并制作出如下的不完整的统计表和统计图,如图所示.请根据图表信息解答以下问题.
组别 | 成绩 | 频数 |
A组 |
|
|
B组 |
| 12 |
C组 |
| 18 |
D组 |
| 21 |
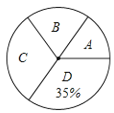
(1)表中一共抽取了________个参赛学生的成绩;![]() ________;
________;
(2)求出计算扇形统计图中“![]() ”的圆心角度数.
”的圆心角度数.
(3)若成绩在90分以上(包括90分)的为“优”等,已知该校共有1200名学生,请你估计该校约有多少名学生的成绩是“优”等.
【题目】某校组织了全校1500名学生参加传统文化知识网络竞赛.赛后随机抽取了其中200名学生的成绩作为样本进行整理,并制作了如下不完整的频数分布表和频数分布直方图.
成绩(分) | 频数(人) | 频率 |
50≤x<60 | 10 | 0.05 |
60≤x<70 | 20 | n |
70≤x<80 | m | 0.15 |
80≤x<90 | 80 | 0.40 |
90≤x<100 | 60 | 0.30 |
请根据图表提供的信息,解答下列各题:
(1)表中m= ,n= ,请补全频数分布直方图;
(2)若用扇形统计图来描述成绩分布情况,则分数段80≤x<90对应扇形的圆心角的度数是 ;
(3)若成绩在80分以上(包括80分)为合格,则参加这次竞赛的1500名学生中成绩合格的大约有多少名?