Question

【题目】如图，在△ABC中，AD是它的角平分线，G是AD上的一点，BG，CG分别平分∠ABC，∠ACB，GH⊥BC，垂足为H，求证：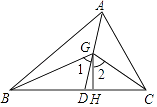
（1）∠BGC=90°+ ∠BAC；
（2）∠1=∠2．

Answer 1

【答案】
（1）解：由三角形内角和定理可知：∠ABC+∠ACB=180°﹣∠BAC，

∵BG，CG分别平分∠ABC，∠ACB，

∠GBC= ∠ABC，∠GCB= ∠ACB

∴∠GBC+∠GCB= （∠ABC+∠ACB）= （180°﹣∠BAC）=90°﹣ ∠BAC

∴∠BGC=180°﹣（∠GBC+∠GCB）=180°﹣ （∠ABC+∠ACB）=90°+ ∠BAC；

（2）解：∵AD是它的角平分线，

∴∠BAD=∠CAD

∴∠1=∠BAD+∠ABG，

∵GH⊥BC，

∴∠GHC=90°

∴∠2=90°﹣∠GCH

=90°﹣ ∠ACB

=90°﹣ （180°﹣∠DAC﹣∠ADC）

= ∠DAC+ ∠ADC

∵∠ADC=∠ABC+∠BAD，

∴ ∠ADC= ∠ABC+∠ ∠BAD

=∠ABG+ ∠BAD，

∴∠2= ∠DAC+ ∠ADC

= ∠BAD+ ∠BAD+∠ABG

=∠BAD+∠ABG，

∴∠1=∠2，

【解析】（1）由三角形内角和定理可知∠ABC+∠ACB=180°﹣∠BAC，然后利用角平分线的性质即可求出∠BGC=90°+ ∠BAC．（2）由于AD是它的角平分线，所以∠BAD=∠CAD，然后根据图形可知：∠1=∠BAD+∠ABG，∠2=90°﹣∠GCH，最后根据三角形的内角和定理以及外角的性质即可求出答案．
【考点精析】掌握三角形的内角和外角是解答本题的根本，需要知道三角形的三个内角中，只可能有一个内角是直角或钝角；直角三角形的两个锐角互余；三角形的一个外角等于和它不相邻的两个内角的和；三角形的一个外角大于任何一个和它不相邻的内角．