题目内容
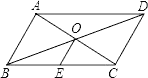
【题目】如图，在直角梯形
中， 
∥
，∠
=90°，
=28cm， 
=24cm， 
=4cm，点
从点
出发，以1cm/s的速度向点
运动，点
从点
同时出发，以2cm/s的速度向点
运动，当其中一个动点到达端点停止运动时，另一个动点也随之停止运动。则四边
的面积
（cm2）与两动点运动的时间
（s）的函数图象大致是（ ）
A. 
B. 
C. 
D. 
【答案】D
【解析】因为在直角梯形ABCD中,DC∥AB,∠A=90°，
所以四边形ANMD也是直角梯形,因此它的面积为12(DM+AN)×AD，
因为DM=t，AN=282t，AD=4；
所以四边形AMND的面积y=12(t+282t)×4=2t+56.
因为当其中一个动点到达端点停止运动时，另一个动点也随之停止运动；
所以当N点到达A点时，2t=28，t=14；
所以自变量t的取值范围是0<t<14.
故选D.
练习册系列答案
相关题目
