题目内容
【题目】为了解家长对“学生在校带手机”现象的看法，某校“九年级兴趣小组”随机调查了该校学生家长若干名，并对调查结果进行整理，绘制如下不完整的统计图：
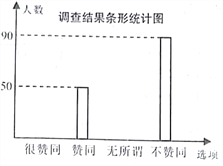
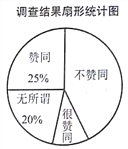
请根据以上信息，解答下列问题
(1)这次接受调查的家长总人数为________人；
(2)在扇形统计图中，求“很赞同”所对应的扇形圆心角的度数；
(3)若在这次接受调查的家长中，随机抽出一名家长，恰好抽到“无所谓”的家长概率是多少?
【答案】200（人）
【解析】试题分析：（1）观察统计图，利用赞同的人数除以它所占的百分比即可得到调查的总人数；
（2）先算出“无所谓”的人数，用总人数分别减去赞同、无所谓、反对的家长人数即可得到“很赞同”态度的学生家长数，再计算出它所占的百分比；
（3）根据概率公式计算即可．
试题解析：解：（1）50÷25%=200（人），所以这次调查的学生家长总人数为200；
（2）“无所谓”人数=200×20%=40（人）
∴“很赞同”人数=200－50－40－90=20（人）
∴“很赞同”对应的扇形圆心角=
×360°=36°
（3）∵“无所谓”的家长人数=40，∴抽到“无所谓”的家长概率=
．
【题目】某公司推出一款产品，经市场调查发现，该产品的日销售量y（个）与销售单价x（元）之间满足一次函数关系．关于销售单价，日销售量，日销售利润的几组对应值如下表：
销售单价x（元） | 85 | 95 | 105 | 115 |
日销售量y（个） | 175 | 125 | 75 | m |
日销售利润w（元） | 875 | 1875 | 1875 | 875 |
（注：日销售利润=日销售量×（销售单价﹣成本单价））
（1）求y关于x的函数解析式（不要求写出x的取值范围）及m的值；
（2）根据以上信息，填空：
该产品的成本单价是 元，当销售单价x= 元时，日销售利润w最大，最大值是 元；
（3）公司计划开展科技创新，以降低该产品的成本，预计在今后的销售中，日销售量与销售单价仍存在（1）中的关系．若想实现销售单价为90元时，日销售利润不低于3750元的销售目标，该产品的成本单价应不超过多少元？
【题目】近年来，共享单车逐渐成为高校学生喜爱的“绿色出行”方式之一，自2016年国庆后，许多高校均投放了使用手机支付就可随取随用的共享单车．某高校为了解本校学生出行使用共享单车的情况，随机调查了某天部分出行学生使用共享单车的情况，并整理成如下统计表．
使用次数 | 0 | 1 | 2 | 3 | 4 | 5 |
人数 | 11 | 15 | 23 | 28 | 18 | 5 |
（1）这天部分出行学生使用共享单车次数的中位数是 ，众数是 ，该中位数的意义是 ；
（2）这天部分出行学生平均每人使用共享单车约多少次？（结果保留整数）
（3）若该校某天有1500名学生出行，请你估计这天使用共享单车次数在3次以上（含3次）的学生有多少人？
【题目】王师傅非常喜欢自驾游，为了解他新买的轿车的耗油情况，将油箱加满后进行了耗油实验，得到下表中的数据：
轿车行驶的路程 |
|
|
|
|
| ······ |
油箱中的剩余油量 |
|
|
|
|
| ····· |
（1）在这个问题中，自变量是_ 因变量是_ ；
（2）该轿车油箱的容量为__ L，行驶
时，估计油箱中的剩余油量为____
；
（3）王师傅将油箱加满后，驾驶该轿车从
地前往
地，到达地时油箱中的剩余油量为
，请估计
两地之间的距离．
【题目】惠民超市第一次用6000元购进甲、乙两种商品，其中乙商品的件数比甲商品件数的
多40件，甲、乙两种商品的进价和售价如下表：（注：获利=售价-进价）
甲种商品 | 乙种商品 | |
进价（元/件） | 22 | 30 |
售价（元/件） | 29 | 40 |
（1）惠民超市购进甲、乙两种商品各多少件?
（2）惠民超市将第一次购进的甲、乙两种商品全部卖完后一共可获利润多少元?
（3）惠民超市第二次以第一次的进价又购进甲、乙两种商品，其中甲商品的件数不变，乙商品的件数是第一次的3倍；甲商品每件降价1元销售，乙商品打折销售，第二次两种商品都销售完以后获得的总利润比第一次获得的总利润多570元，求第二次乙商品是按原价打几折销售?
