题目内容
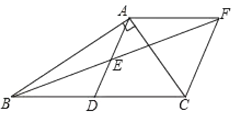
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 边的中点,过点
边的中点,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,
,![]() 平分
平分![]() 交
交![]() 于点
于点![]() .
.

(1)求证:判断四边形![]() 的形状,并证明;
的形状,并证明;
(2)若![]() ,求
,求![]() 及四边形
及四边形![]() 的面积.
的面积.
【答案】(1)是平行四边形,详见解析;(2)12
【解析】
(1)根据等腰直角三角形性质得∠ABC=∠BAC=45°,根据垂直定义得∠ECB=∠CBF=45°,证△CED≌△BDF(ASA),推出ED=FD,CD=BD即可;
(2)延长CE与AB相交于H,根据勾股定理求出CD,AC和AB,推出EH是△ABF的中位线,根据中位线性质得到BF=2EH,AE=EF,根据勾股定理求出EH,根据平行四边形面积公式直接再求解.
解:(1)四边形![]() 是平行四边形,理由:
是平行四边形,理由:
∵在△ABC中,![]() ,AC=BC,
,AC=BC,
∴∠ABC=∠BAC=45°
∵D是BC中点
∴CD=BD
∵BF⊥AB
∴∠ABF=90°
∴∠CBF=90°-45°=45°
∵CE平分∠ACB
∴∠ECB=∠CBF=45°
在△CED和△BFD中

∴△CED≌△BDF(ASA)
∴ED=FD
又CD=BD
∴四边形![]() 是平行四边形
是平行四边形
(2)延长CE与AB相交于H
设CD=x,则AC=BC=2x
在直角三角形ADC中
![]()
解得x=3
∴AC=6
∴AB=![]()
∵AC=BC,CE平分∠ACB
∴CH⊥AB,BH=![]()
又∵![]()
∴EH∥BF
∴EH是△ABF的中位线
∴BF=2EH,AE=EF
又∵ED=DF
∴AE=![]()
∴EH=
∴BF=2EH=2![]()
∴平行四边形![]() 的面积:BFBH=
的面积:BFBH=![]()
![]()

练习册系列答案
相关题目