题目内容
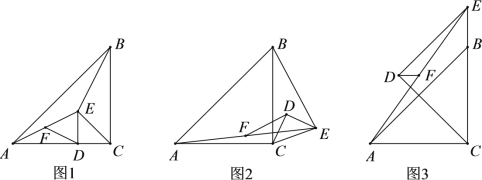
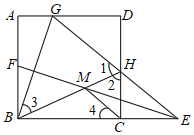
【题目】如图,正方形ABCD中,E是BC延长线上一点,在AB上取一点F,使点B关于直线EF的对称点G落在AD上,连接EG交CD于点H,连接BH交EF于点M,连接CM.则下列结论,其中正确的是( )
①∠1=∠2;
②∠3=∠4;
③GD=![]() CM;
CM;
④若AG=1,GD=2,则BM=![]() .
.
A.①②③④B.①②C.③④D.①②④
【答案】A
【解析】
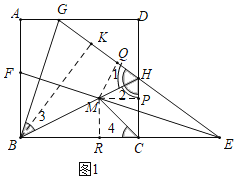
①正确.如图1中,过点B作BK⊥GH于K.想办法证明Rt△BHK≌Rt△BHC(HL)可得结论.
②正确.分别证明∠GBH=45°,∠4=45°即可解决问题.
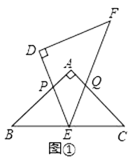
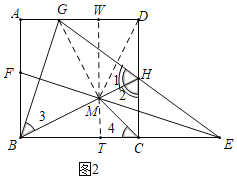
③正确.如图2中,过点M作MW⊥AD于W,交BC于T.首先证明MG=MD,再证明△BTM≌△MWG(AAS),推出MT=WG可得结论.
④正确.求出BT=2,TM=1,利用勾股定理即可判断.
解:如图1中,过点B作BK⊥GH于K.
∵B,G关于EF对称,
∴EB=EG,
∴∠EBG=∠EGB,
∵四边形ABCD是正方形,
∴AB=BC,∠A=∠ABC=∠BCD=90°,AD∥BC,
∴∠AGB=∠EBG,
∴∠AGB=∠BGK,
∵∠A=∠BKG=90°,BG=BG,
∴△BAG≌△BKG(AAS),
∴BK=BA=BC,∠ABG=∠KBG,
∵∠BKH=∠BCH=90°,BH=BH,
∴Rt△BHK≌Rt△BHC(HL),
∴∠1=∠2,∠HBK=∠HBC,故①正确,
∴∠GBH=∠GBK+∠HBK=![]() ∠ABC=45°,
∠ABC=45°,
过点M作MQ⊥GH于Q,MP⊥CD于P,MR⊥BC于R.
∵∠1=∠2,
∴MQ=MP,
∵∠MEQ=∠MER,
∴MQ=MR,
∴MP=MR,
∴∠4=∠MCP=![]() ∠BCD=45°,
∠BCD=45°,
∴∠GBH=∠4,故②正确,
如图2中,过点M作MW⊥AD于W,交BC于T.
∵B,G关于EF对称,
∴BM=MG,
∵CB=CD,∠4=∠MCD,CM=CM,
∴△MCB≌△MCD(SAS),
∴BM=DM,
∴MG=MD,
∵MW⊥DG,
∴WG=WD,
∵∠BTM=∠MWG=∠BMG=90°,
∴∠BMT+∠GMW=90°,
∵∠GMW+∠MGW=90°,
∴∠BMT=∠MGW,
∵MB=MG,
∴△BTM≌△MWG(AAS),
∴MT=WG,
∵MC=![]() TM,DG=2WG,
TM,DG=2WG,
∴DG=![]() CM,故③正确,
CM,故③正确,
∵AG=1,DG=2,
∴AD=AB=TM=3,EM=WD=TM=1,BT=AW=2,
∴BM=![]() ,故④正确,
,故④正确,
故选:A.