题目内容
【题目】有这样一个问题:探究同一坐标系中系数互为倒数的正、反比例函数![]() 与
与![]() 的图象性质.小明根据学习函数的经验,对函数
的图象性质.小明根据学习函数的经验,对函数![]() 与
与![]() ,当k>0时
,当k>0时![]() 的图象性质进行了探究,下面是小明的探究过程:
的图象性质进行了探究,下面是小明的探究过程:
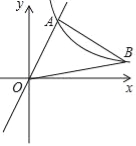
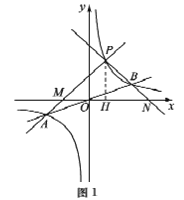
(1)如图所示,设函数![]() 与
与![]() 图像的交点为A,B.已知A的坐标为(-k,-1),则B点的坐标为 .
图像的交点为A,B.已知A的坐标为(-k,-1),则B点的坐标为 .
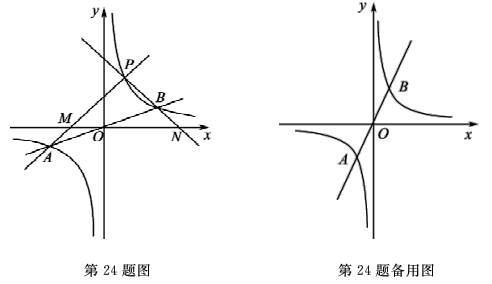
(2)若P点为第一象限内双曲线上不同于点B的任意一点.
①设直线PA交x轴于点M,直线PB交x轴于点N.求证:PM=PN.
证明过程如下:设P(m,![]() ),直线PA的解析式为y=ax+b(a≠0).
),直线PA的解析式为y=ax+b(a≠0).
则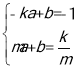 解得
解得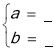
所以,直线PA的解析式为 .
请把上面的解答过程补充完整,并完成剩余的证明.
②当P点坐标为(1,k)(k≠1)时,判断ΔPAB的形状,并用k表示出ΔPAB的面积.
【答案】(1)(k,1);(2)①证明见解析;②ΔPAB为直角三角形.![]() 或
或![]() .
.
【解析】
试题分析:(1)利用反比例函数的对称性指:A点和B点关于原点对称,从而求出B(k,1)
(2)①解方程组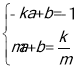 ,直线PA的解析式为
,直线PA的解析式为![]() ,求出M(m-k,0);同理求出:N(m+k,0),作PH⊥x轴,得H(m,0),∴MK=NK=k,最后利用线段垂直平分线线定理知PM=PN.
,求出M(m-k,0);同理求出:N(m+k,0),作PH⊥x轴,得H(m,0),∴MK=NK=k,最后利用线段垂直平分线线定理知PM=PN.
②分两种情况讨论:第一:当k>1时,![]() ;
;
第二:当0<k<1时,![]() .
.
试题解析:(1)B点的坐标为(k,1)
(2)①证明过程如下:设P(m,![]() ),直线PA的解析式为y=ax+b(a≠0).
),直线PA的解析式为y=ax+b(a≠0).
则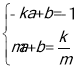 解得
解得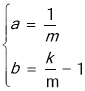
所以,直线PA的解析式为![]() .
.
令y=0,得x=m-k
∴M点的坐标为(m-k,0)
过点P作PH⊥x轴于H
∴点H的坐标为(m,0)
∴MH=xH-xM=m-(m-k)=k.
同理可得:HN=k
∴PM=PN
②由①知,在ΔPMN中,PM=PN
∴ΔPMN为等腰三角形,且MH=HN=k
当P点坐标为(1,k)时,PH=k
∴MH=HN=PH
∴∠PMH=∠MPH=45°,∠PNH=∠NPH=45°
∴∠MPN=90°,即∠APB=90°
∴ΔPAB为直角三角形.
当k>1时,如图1,![]()
=![]()
=![]()
![]()
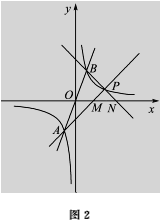
当0<k<1时,如图2,
![]()
![]()
=![]()
=![]()

 名校课堂系列答案
名校课堂系列答案