题目内容
 如图,已知等边△ABC,以BC为直径作半⊙O交AB于D,DE⊥AC于点E.
如图,已知等边△ABC,以BC为直径作半⊙O交AB于D,DE⊥AC于点E.
(1)求证:DE是半⊙O的切线;
(2)若DE= ,求△ABC与半⊙O重合部分的面积.
,求△ABC与半⊙O重合部分的面积.
 (1)证明:连接OD,CD,
(1)证明:连接OD,CD,∵△ABC为等边三角形,
∴AC=BC,
∵BC为圆O的直径,
∴∠BDC=90°,
∴CD⊥AB,
∴D为AB的中点,
又O为BC的中点,
∴OD为△ABC的中位线,
∴OD∥AC,
∵DE⊥AC,
∴DE⊥OD,
则DE与圆O相切;
(2)解:连接BF,OF,由(1)同理得到OF∥AB,
∵△ABC为等边三角形,
∴∠ABC=∠ACB=60°,
∴∠FOC=∠DOB=60°,
∴∠DOF=60°,
∵DE⊥AC,BF⊥AC,
∴DE∥BF,
∵D为AB的中点,
∴E为AF中点,即DE为△ABF的中位线,
∴BF=2DE=2
 ,
,在Rt△BCF中,∠CBF=30°,
设CF=x,则BC=2x,
根据勾股定理得:(2
 )2+x2=(2x)2,
)2+x2=(2x)2,解得:x=2,
∴等边△BOD和△COF边长都为2,半圆半径为2,
则△ABC与半圆O重合部分的面积S=2S△BOD+S扇形DOF=2×
 ×4+
×4+ =2
=2 +
+ .
.分析:(1)连接OD,CD,由三角形ABC为等边三角形,得到AC=BC,再由直径所对的圆周角为直角得到CD垂直于AB,利用三线合一得到D为AB的中点,由O为BC中点,得到OD为三角形ABC的中位线,利用中位线定理得到OD与AC平行,由DE垂直于AC,得到DE垂直于OD,可得出DE与圆O相切;
(2)连接BF,OF,由(1)同理得到OF为三角形ABC的中位线,即OF平行与AB,由等边三角形的内角为60度得到∠ABC与∠ACB为60度,利用两直线平行同位角相等得到∠BOD与∠COF都为60度,可得出三角形BOD与三角形COF都为等边三角形,扇形DOF的圆心角为60,由DE与BF都与AC垂直得到DE与BF平行,D为AB中点,可得出E为AF中点,利用中位线定理得到BF=2DE,求出BF的长,即为等边三角形的高,在直角三角形BCF中,设CF=x,可得出BC=2x,根据勾股定理列出关于x的方程,求出方程的解得到x的值,确定出等边三角形BOD与COF的边长与扇形的半径,由两小等边三角形的面积加上扇形的面积即可求出三角形ABC与半圆重合的面积.
点评:此题考查了切线的判定,等边三角形的判定与性质,圆周角定理,三角形的中位线定理,以及扇形面积的求法,熟练掌握切线的判定方法是解本题的关键.

练习册系列答案
相关题目
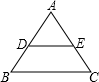
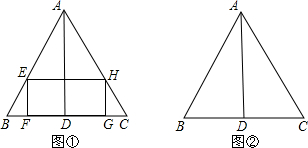
 (2013•黄浦区二模)如图,已知等边△ABC的边长为1,设
(2013•黄浦区二模)如图,已知等边△ABC的边长为1,设
 如图,已知等边三角形ABC的边长为10,点P、Q分别为边AB、AC上的一个动点,点P从点B出发以1cm/s的速度向点A运动,点Q从点C出发以2cm/s的速度向点A运动,连接PQ,以Q为旋转中心,将线段PQ按逆时针方向旋转60°得线段QD,若点P、Q同时出发,则当运动
如图,已知等边三角形ABC的边长为10,点P、Q分别为边AB、AC上的一个动点,点P从点B出发以1cm/s的速度向点A运动,点Q从点C出发以2cm/s的速度向点A运动,连接PQ,以Q为旋转中心,将线段PQ按逆时针方向旋转60°得线段QD,若点P、Q同时出发,则当运动