题目内容
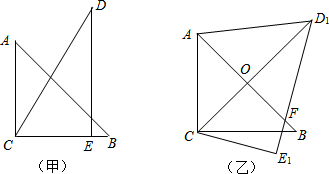
18.如图,将三角形纸片ABC(AB>AC)沿过点A的直线折叠,使得AC边落在AB边上,折痕为AD,展开纸片(如图①);再次折叠该三角形纸片,使点A和点D重合,折痕为EF,展开后得到△AEF(如图②).EF与AD交于点O.求证:△AEF为等腰三角形.

(1)下框中是小明对此题的解答.

小明的解答是否正确?如果不正确,请用圈出他解答过程中发生错误的步骤,指出错误的原因并完成正确的解答.
(2)如图③,在图②中连接DE、DF.求证:四边形AEDF是菱形.
分析 (1)小明的解答错误,利用三角形的内角和可以得出∠AEF=∠AFE,所以△AEF为等腰三角形;
(2)根据四边相等的四边形是菱形得结论.
解答 解:(1)小明的解答错误.因为由折叠无法得到OE=OF,
由折叠知,AD平分∠BAC,所以∠BAD=∠CAD,
又由折叠知,∠AOE=∠AOF=90°,
∴∠AEF=∠AFE,
∴AE=AF,即△AEF为等腰三角形;
(2)由折叠知,EA=ED,FA=FD,
由(1)知AE=AF,
∴EA=ED=FA=FD,
∴四边形AEDF是菱形.
点评 本题考查了菱形的性质和判定、折叠的性质,明确折叠前后的两条边相等,两个角相等;并熟练掌握菱形的判定,常用的判定方法为:四边相等的四边形是菱形.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
13.一元二次方程3x2-2x+3=0的根的情况是( )
| A. | 有两个不相等的正实数根 | B. | 有两个异号实数根 | ||
| C. | 有两个相等的正实数根 | D. | 没有实数根 |
8.下列图形既是轴对称图形,又是中心对称图形的有( )个
①等边三角形 ②菱形 ③圆 ④正六边形 ⑤抛物线.
①等边三角形 ②菱形 ③圆 ④正六边形 ⑤抛物线.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
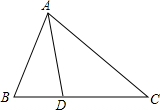 如图,已知∠BAC=60°,D是△ABC的边BC上的一点,且∠CAD=∠C,∠ADB=80°.求∠B的度数.
如图,已知∠BAC=60°,D是△ABC的边BC上的一点,且∠CAD=∠C,∠ADB=80°.求∠B的度数.
 如图,平面直角坐标系中有点B(-1,0)和y轴上一动点A(0,a),其中a>0,以A点为直角顶点在第二象限内作等腰直角△ABC,设点C的坐标为(c,d).
如图,平面直角坐标系中有点B(-1,0)和y轴上一动点A(0,a),其中a>0,以A点为直角顶点在第二象限内作等腰直角△ABC,设点C的坐标为(c,d). 如图,直线l的解析式为y=-$\frac{4}{3}$x+4,它与坐标轴分别交于A、B两点.
如图,直线l的解析式为y=-$\frac{4}{3}$x+4,它与坐标轴分别交于A、B两点.