Question

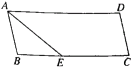
【题目】如图，ABCD中，点E是CD延长线上一点，BE交AD于点F，DE=CD．

（1）求证：△ABF∽△CEB

（2）若△DEF的面积为2，求ABCD的面积．

（3）若G、H分别为BF、AB的中点，AG、FH交于点O，求．

Answer 1

【答案】（1）证明见解析；（2）24；（3）1:2.

【解析】

(1)由ABCD可知AB∥CD且∠BAD=∠C，据此可进行证明；

(2)先证明△DFD分别与△BAF、△EBC相似，利用相似比分别求出S△BFA和S梯形FDBC的面积；

(3)由G、H分别为BF、AB的中点可知GH为中位线，进而可证明△OHG∽△OAF并进行求解.

（1）证明：∵ABCD，

∴AB∥CE，AD∥BC，

∴∠ABF=∠E，

又∵ABCD是平行四边形，

∴∠BAF=∠C，

△ABF∽△CEB，

（2）解：∵∠ABF=∠E，∠AFB=∠EFD，

∴△ABF∽△DEF，

∵AD∥BC，

∴△CEB∽△DEF，

∵DE=CD，

∴，，

∴，，

∵△DEF的面积为2，

∴S△BFA=8，S△EBC=18，

∴S梯形FDBC=18﹣2=16，

∴S平行四边形ABCD=16+8=24，

（3）解：∵G、H为中点，

∴GH∥AF，2GH=AF，

∴OG：OA=HG：AF=1：2．