题目内容
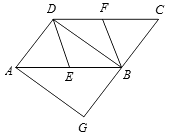
【题目】如图，在平行四边形 
中， 
分别为边 
的中点， 
是对角线，过点 
作 
交 
的延长线于点 
．
（1）求证： 
；
（2）若 
，求证：四边形 
是菱形．
【答案】
（1）
证明：（1）在平行四边形ABCD 中，AB∥CD，AB=CD
∵E、F分别为AB、CD的中点
∴DF= 
DC，BE= AB
∴DF∥BE，DF=BE
∴四边形DEBF为平行四边形，
∴DE∥BF；
（2）
∵AG∥BD，
∴∠G=∠DBC=90°，
∴△DBC 为直角三角形，
又∵F为边CD的中点，
∴BF= DC=DF，
又∵四边形DEBF为平行四边形，
∴四边形DEBF是菱形．
【解析】1）根据已知条件证明BE=DF，BE∥DF，从而得出四边形DFBE是平行四边形，即可证明DE∥BF，（2）先证明DE=BE，再根据邻边相等的平行四边形是菱形，从而得出结论．
【考点精析】关于本题考查的平行四边形的判定和菱形的判定方法，需要了解两组对边分别平行的四边形是平行四边形：两组对边分别相等的四边形是平行四边形；一组对边平行且相等的四边形是平行四边形；两组对角分别相等的四边形是平行四边形；对角线互相平分的四边形是平行四边形；任意一个四边形，四边相等成菱形；四边形的对角线，垂直互分是菱形．已知平行四边形，邻边相等叫菱形；两对角线若垂直，顺理成章为菱形才能得出正确答案．
练习册系列答案
相关题目
