题目内容
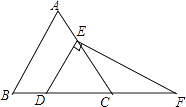
【题目】若点A(3,3 )是正比例函数y=x上一点,点M(m,0)与点N(0,n)分别在x轴与y轴上,且∠MAN=90°.
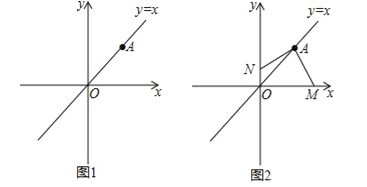
(1)如图1,当N点与原点O重合,求M点的坐标;
(2)如图2,已知m,n都为正数,连接MN,若MN=![]() ,求△MON的面积.
,求△MON的面积.
【答案】(1)M(6,0);(2)![]() .
.
【解析】
试题分析:(1)过点A作AD⊥x轴于D,由点A的坐标即可得出AD=OD=3,进而得出∠AOD=∠OAD=45°,再通过角的计算得出∠AMO=45°,从而得出AO=AM,根据等腰三角形的性质即可得出OM=2OD,由此即可得出点M的坐标;
(2)过点A作AQ⊥x轴于Q,作AP⊥y轴于P,由点A的坐标结合矩形的性质即可得出四边形APOQ是正方形,根据正方形的性质找出AP=AQ,再根据全等三角形的判定定理(ASA)即可证出△APN≌△AQM,从而得出PN=QM,通过边与边之间的关系结合勾股定理即可得出mn的值,将其代入三角形的面积公式即可得出结论.
试题解析:(1)当N点与原点O重合时,过点A作AD⊥x轴于D,如图3所示.
∵A(3,3),∴AD=OD=3,∴∠AOD=∠OAD=45°.
又∵∠MAN=90°,∴∠AMO=90°﹣45°=45°,∴AO=AM,∴OM=2OD=6,∴M点坐标为(6,0).
(2)过点A作AQ⊥x轴于Q,作AP⊥y轴于P,如图4所示.
则∠APO=∠AQO=90°,又∵∠POQ=90°,∴四边形APOQ是矩形,∵A(3,3),∴OP=OQ=3,∴四边形APOQ是正方形,∴AP=AQ.
∵∠PAN+∠NAQ=90°,∠QAM+∠NAQ=90°,∴∠PAN=∠QAM.
在△APN和△AQM中,∵∠APN=∠AQM=90°,AP=AQ,∠PAN=∠QAM,∴△APN≌△AQM(ASA),∴PN=QM.
∵M (m,0),N (0,n),∴ON=n,OM=m,∴PN=3﹣n,QM=m﹣3,∴3﹣n=m﹣3,即m+n=6.
在Rt△MON中,OM2+ON2=MN2,∴![]() ,即m2+n2=30.
,即m2+n2=30.
∵(m+n)2=m2+2mn+n2,∴62=30+2mn,即mn=3,∴![]() =
=![]() =
=![]() .
.

【题目】某商场一天中售出李宁牌运动鞋11双,其中各种尺码的鞋的销售量如表所示,则这11双鞋的尺码组成一组数据中位数为_____.
鞋的尺码(单位:厘米) | 23.5 | 24 | 24.5 | 25 | 26 |
销售量(单位:双) | 1 | 2 | 2 | 5 | 1 |
【题目】某商场用2500元购进A、B两种新型节能台灯共50盏,这两种台灯的进价、标价如下表所示.
类型 | A型 | B型 |
进价(元/盏) | 40 | 65 |
标价(元/盏) | 60 | 100 |
(1)这两种台灯各购进多少盏?
(2)若A型台灯按标价的9折出售,B型台灯按标价的8折出售,那么这批台灯全部售出后,商场共获利多少元?