题目内容
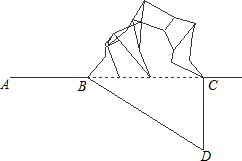 市政府为改善我市的交通状况,促进经济发展,在“温泉--崇阳”路段间修建了“翠竹岭”隧道.如图,隧道BC沿直线ABC打通,测得∠ABD=167.2°,BD=600m,∠D=77.2度.已知汽车走隧道的耗油量为0.2升/km,走原山坡公路的耗油量为0.6升/km.隧道长与山坡公路长的比为1:10,那么汽车每通过“翠竹岭”一次,走隧道比走山坡公路节省油料多少升(精确到0.1升)?
市政府为改善我市的交通状况,促进经济发展,在“温泉--崇阳”路段间修建了“翠竹岭”隧道.如图,隧道BC沿直线ABC打通,测得∠ABD=167.2°,BD=600m,∠D=77.2度.已知汽车走隧道的耗油量为0.2升/km,走原山坡公路的耗油量为0.6升/km.隧道长与山坡公路长的比为1:10,那么汽车每通过“翠竹岭”一次,走隧道比走山坡公路节省油料多少升(精确到0.1升)?
(参考数据:sin12.8°=0.2215,sin77.2°=0.9750,cos12.8°=0.9750,cos77.2°=0.2215)
解:在直角△BCD中,
∵BC=BD•cos12.8°
=600×0.9750
=585m
=0.585km.
∴走隧道时的油耗是0.585×0.2=0.117升.
走山坡公路的路程是0.585×10=5.85km,
∴油耗是5.85×0.6=3.51升.
因而走隧道比走山坡公路节省油料3.51-0.117=3.393升.
分析:由于∠ABD=167.2°,可以得到∠D=77.2°,又根据已知条件知道△BCD是直角三角形,由此就可以求出隧道长,进而得到山坡公路的长,然后算出各自的油耗就可以得到省油料多少升.
点评:此题首先要把实际问题转化成数学问题,然后利用直角三角形的性质,三角函数的性质解题.
∵BC=BD•cos12.8°
=600×0.9750
=585m
=0.585km.
∴走隧道时的油耗是0.585×0.2=0.117升.
走山坡公路的路程是0.585×10=5.85km,
∴油耗是5.85×0.6=3.51升.
因而走隧道比走山坡公路节省油料3.51-0.117=3.393升.
分析:由于∠ABD=167.2°,可以得到∠D=77.2°,又根据已知条件知道△BCD是直角三角形,由此就可以求出隧道长,进而得到山坡公路的长,然后算出各自的油耗就可以得到省油料多少升.
点评:此题首先要把实际问题转化成数学问题,然后利用直角三角形的性质,三角函数的性质解题.

练习册系列答案
相关题目
 .
. a2b3和-a3b2的共同点填写在下列横线上:
a2b3和-a3b2的共同点填写在下列横线上: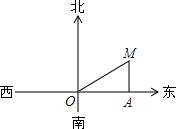 如图,上午8:00时,一船在某灯塔O的正东方向5海里的A处向正北方向航行,上午10:00,船离灯塔O的距离MO=13海里,求此船航行的速度.
如图,上午8:00时,一船在某灯塔O的正东方向5海里的A处向正北方向航行,上午10:00,船离灯塔O的距离MO=13海里,求此船航行的速度.
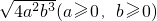
 .
.
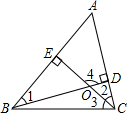 如图所示,BD,CE是△ABC的两条高,它们的交点为O.
如图所示,BD,CE是△ABC的两条高,它们的交点为O.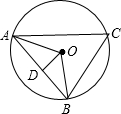 如图,AB是⊙O的弦,OD⊥AB于点D,C是AB优弧上任意一点,则图中所有相等的线段有________;所有相等的角有________.
如图,AB是⊙O的弦,OD⊥AB于点D,C是AB优弧上任意一点,则图中所有相等的线段有________;所有相等的角有________.